Question

A differentiable function $f$ satisfies the relation $f(x+y)=f(x)+f(y)+2xy(x+y)-\frac{1}{3}\forall x,y \in R$ and $lim_{h\to 0}(\frac{3f(h)-1}{6h})=\frac{2}{3}$ then value of $[f(2)]$ is, where [.] denote GIF

Answer 1

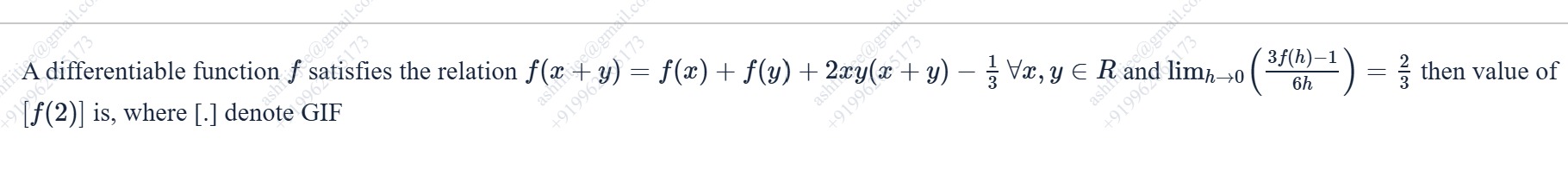
8

Answer 2

Let the given functional equation be $f(x+y) = f(x) + f(y) + 2xy(x+y) - \frac{1}{3} \quad (*)$. This relation holds for all $x, y \in R$. The function $f$ is differentiable.

First, let's find the value of $f(0)$. Set $x=0$ and $y=0$ in the functional equation $(*)$: $f(0+0) = f(0) + f(0) + 2(0)(0)(0+0) - \frac{1}{3}$ $f(0) = 2f(0) - \frac{1}{3}$ $f(0) = \frac{1}{3}$.

Next, we use the given limit condition: $\lim_{h\to 0} \left(\frac{3f(h)-1}{6h}\right) = \frac{2}{3}$ We know $f(0) = \frac{1}{3}$, so $3f(0) = 1$. The limit can be rewritten as: $\lim_{h\to 0} \left(\frac{3f(h)-3f(0)}{6h}\right) = \frac{2}{3}$ $\frac{3}{6} \lim_{h\to 0} \left(\frac{f(h)-f(0)}{h}\right) = \frac{2}{3}$ $\frac{1}{2} f'(0) = \frac{2}{3}$ $f'(0) = \frac{4}{3}$.

Now we need to find the derivative of $f(x)$. We can use the definition of the derivative: $f'(x) = \lim_{h\to 0} \frac{f(x+h)-f(x)}{h}$ From the functional equation $(*)$, set $y=h$: $f(x+h) = f(x) + f(h) + 2xh(x+h) - \frac{1}{3}$ So, $f(x+h) - f(x) = f(h) + 2xh(x+h) - \frac{1}{3}$. Substitute this into the definition of the derivative: $f'(x) = \lim_{h\to 0} \frac{f(h) + 2xh(x+h) - \frac{1}{3}}{h}$ $f'(x) = \lim_{h\to 0} \left(\frac{f(h)-\frac{1}{3}}{h} + \frac{2xh(x+h)}{h}\right)$ Since $f(0) = \frac{1}{3}$, we have $\frac{f(h)-\frac{1}{3}}{h} = \frac{f(h)-f(0)}{h}$. $f'(x) = \lim_{h\to 0} \left(\frac{f(h)-f(0)}{h} + 2x(x+h)\right)$ $f'(x) = \lim_{h\to 0} \frac{f(h)-f(0)}{h} + \lim_{h\to 0} 2x(x+h)$ The first limit is $f'(0)$, and the second limit is $2x(x+0) = 2x^2$. $f'(x) = f'(0) + 2x^2$ Substitute the value of $f'(0) = \frac{4}{3}$: $f'(x) = \frac{4}{3} + 2x^2$.

Now, integrate $f'(x)$ to find $f(x)$: $f(x) = \int \left(\frac{4}{3} + 2x^2\right) dx$ $f(x) = \frac{4}{3}x + \frac{2x^3}{3} + C$, where $C$ is the constant of integration.

To find $C$, use the value $f(0) = \frac{1}{3}$: $f(0) = \frac{4}{3}(0) + \frac{2(0)^3}{3} + C$ $\frac{1}{3} = 0 + 0 + C$ $C = \frac{1}{3}$.

So, the function is $f(x) = \frac{2x^3}{3} + \frac{4x}{3} + \frac{1}{3}$.

The question asks for the value of $[f(2)]$, where [.] denotes the Greatest Integer Function (GIF). Calculate $f(2)$: $f(2) = \frac{2(2)^3}{3} + \frac{4(2)}{3} + \frac{1}{3}$ $f(2) = \frac{2(8)}{3} + \frac{8}{3} + \frac{1}{3}$ $f(2) = \frac{16}{3} + \frac{8}{3} + \frac{1}{3}$ $f(2) = \frac{16+8+1}{3} = \frac{25}{3}$.

Now, find the greatest integer of $f(2)$: $[f(2)] = \left[\frac{25}{3}\right]$ $\frac{25}{3} = 8.333...$ The greatest integer less than or equal to $8.333...$ is $8$. $[f(2)] = 8$.