Question

A diet for a sick person must contain at least 4000 units of vitamins, 50 units of minerals and 1400 calories. Two foods X and Y are available at a cost of Rs. 4 and Rs. 3 per unit respectively. One unit of food X contains 200 units of vitamins, 1 unit of minerals and 40 calories, whereas one unit of food Y contains 100 units of vitamins, 2 units of minerals and 40 calories. Find what combination of X and Y should be used to have least cost. Also find the least cost.

Answer 1

We first assume the variables and then convert the given conditions into algebraic forms. We plot those inequalities in the graph to find the intersecting points. Using the least cost equation and those intersecting points we find the solution that satisfies all the conditions.

Complete step by step answer:
We need to find the combination of X and Y to have the least cost.
Let us assume that we need a combination of p units of X and q units of Y to have least cost.
Two foods X and Y are available at a cost of Rs. 4 and Rs. 3 per unit respectively.
So, total cost will be $c=4p+3q$. We need to minimise the cost.
The given conditions are a sick person must have 4000 units of vitamins, 50 units of minerals and 1400 calories where one unit of the food X contains 200 units of vitamins, 1 unit of minerals and 40 calories, whereas one unit of food Y contains 100 units of vitamins, 2 units of minerals and 40 calories.
Forming the inequality for vitamins, we get $200p+100q\ge 4000$.
Dividing with 100 and simplifying we get $2p+q\ge 40$.
Forming the inequality for minerals, we get $p+2q\ge 50$.
Forming the inequality for calories, we get $40p+40q\ge 1400$.
Dividing with 40 and simplifying we get $p+q\ge 35$
We draw the lines on graph to get the intersecting points as $A\left( 0,40 \right)$, $B\left( 5,30 \right)$, $C\left( 20,15 \right)$, $D\left( 50,0 \right)$.

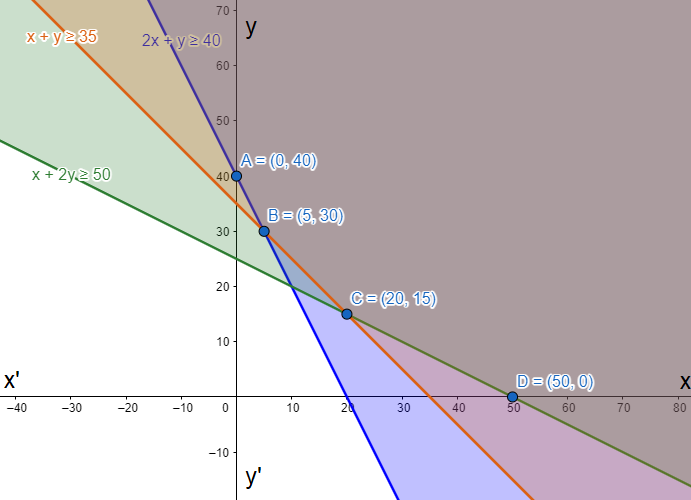
We find the minimum value possible for $c=4p+3q$ at those points.
At $A\left( 0,40 \right)$ we get $c=3\times 40=120$.
At $B\left( 5,30 \right)$ we get $c=4\times 5+3\times 30=110$.
At $C\left( 20,15 \right)$ we get $c=4\times 20+3\times 15=125$.
At $D\left( 50,0 \right)$ we get $c=4\times 50=200$.
So, the least value is achieved at $B\left( 5,30 \right)$.
Therefore, the combination of X and Y that should be used to have the least cost is 5 and 30 units respectively. Also, the least cost is Rs. 110.

Note: We take the origin point in multiplications. We can use any point other than the ones that are on the line itself to find out the direction in which the required region is.
For example, we take the point $\left( -1,-1 \right)$ instead of $\left( 0,0 \right)$. This does not satisfy the inequality $2p+q\ge 40$ where we get $-3\ge 40$. The area goes to the opposite side.
This means we can take any arbitrary point and that will indicate the area accordingly.