Question
Question: A dielectric slab fills the lower half of a parallel plate capacitor as shown in figure: (Take plate...
A dielectric slab fills the lower half of a parallel plate capacitor as shown in figure: (Take plate area as A)
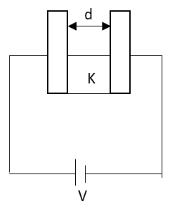
A .equivalent capacity of the system is ((ε0A/2d)(1+K))
B. the net charge of the lower half of the left hand plate is 1/K times the charge on the upper half of the plate
C. net charges on the lower and upper halves of the left hand plate are different
D. the net charge on the lower hand of the left hand plate is 2dKε0A×V
Solution
Use the formula for the capacitance of a parallel plate capacitor. Also use the formula for the charge on the plates of a capacitor. Consider the upper and lower half portions of the capacitor in the figure as two capacitors connected in parallel. Calculate the net capacitance of the two capacitors. Then using the formula for the charge on the capacitor, calculate the charge on the upper and lower halves of the left plate of the capacitor.
Formulae used:
The capacitance C of a parallel plate capacitor is
C=dε0A …… (1)
Here, ε0 is permittivity of free space, A is an area of the capacitor and d is separation between the two plates of the capacitor.
The charge Q on a capacitor is
Q=CV …… (2)
Here, C is capacitance of the capacitor and V is the potential difference between the plates of the capacitor.
Complete step by step answer:
We have given that a dielectric slab is filled in the lower half portion of a parallel plate capacitor.The upper half and lower half of the given system of capacitor can be considered as the two capacitors in parallel.We have given that the total area of the given capacitor is A. Hence, the area of the lower half and upper half of the parallel plate capacitor is 2A.
Hence, the area of the upper half of the capacitor is
C1=2dε0A
The area of the lower half portion of the capacitor is
C2=2dε0KA
Since the two capacitors are in parallel, the equivalent capacitance is
Ceq=C1+C2
⇒Ceq=2dε0A+2dε0KA
⇒Ceq=2dε0A(1+K)
Therefore, the equivalent capacitance of the system is 2dε0A(1+K).
Hence, the option A is correct.
Let us now calculate the charge on the lower half and upper half of the left hand side plate of the capacitor. The potential V on the lower and upper half of the left hand side capacitor is the same. The charge QLU on the upper half of the left hand side capacitor is
QLU=C1V
⇒QLU=2dε0AV ……. (3)
The charge QLL on the upper half of the left hand side capacitor is
QLL=C2V
⇒QLL=2dε0KAV …… (4)
Substitute QLU for 2dε0AV in the above equation.
⇒QLL=KQLU
Therefore, the charge on lower half of the left hand side plate of capacitor is K times the charge on the upper half of the left hand side plate of capacitor.Hence, the option B is incorrect.From equations (3) and (4), we can say that the charges on lower and upper half of the left hand side plate of the capacitor are different.Hence, the option C is correct.
Rewrite equation (4) as
⇒QLL=2dε0KA×V
Therefore, the net charge on the lower half of the left plate of the capacitor is 2dε0KA×V.
Hence, the option D is correct.
Hence, the correct options are A, C and D.
Note: One can also explain the option C by another method. One can explain that the upper and lower half of the left plate of the parallel plate capacitor are in parallel. Hence, the potential difference between them is the same and hence, the charge on these two capacitors in parallel must be different.
