Question

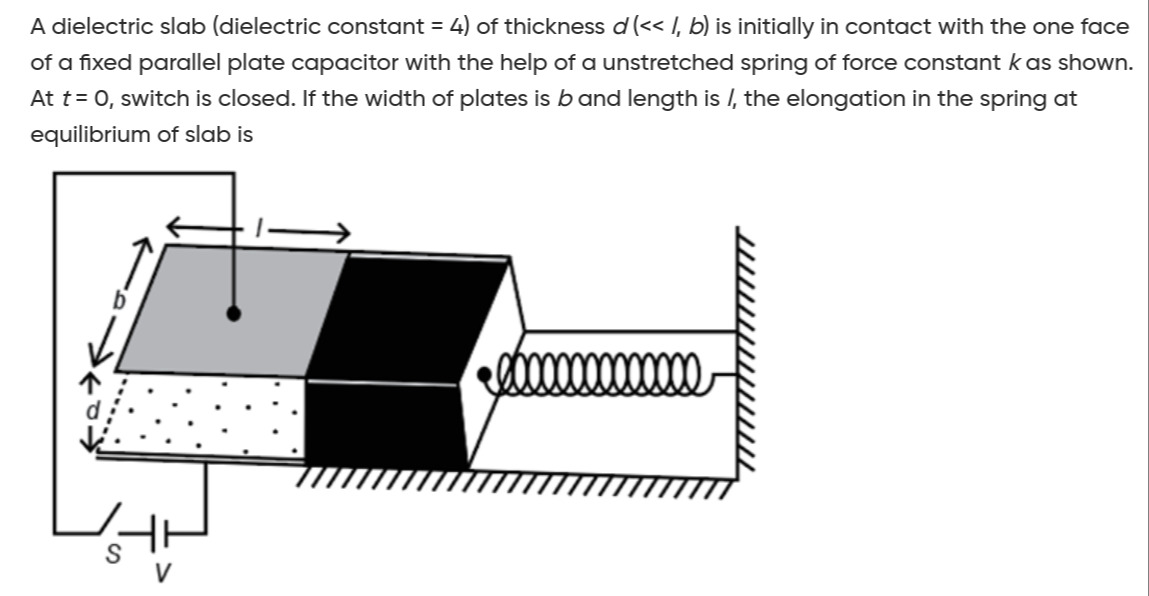
A dielectric slab (dielectric constant = 4) of thickness $d(<< l, b)$ is initially in contact with the one face of a fixed parallel plate capacitor with the help of a unstretched spring of force constant $k$ as shown. At $t = 0$, switch is closed. If the width of plates is $b$ and length is $l$, the elongation in the spring at equilibrium of slab is

Answer 1

x = \frac{3 \epsilon_0 b V^2}{2kd}

Answer 2

The problem describes a parallel plate capacitor with a dielectric slab partially inserted. A battery maintains a constant voltage $V$ across the capacitor, and a spring with constant $k$ opposes the insertion of the dielectric. We need to find the elongation of the spring at equilibrium.

1. Capacitance as a function of insertion length ($x$):

   When the dielectric slab (dielectric constant $\kappa=4$) is inserted by a length $x$, the capacitor can be viewed as two parallel capacitors:

   • One filled with dielectric: Area $xb$, separation $d$. Capacitance $C_1 = \frac{\kappa \epsilon_0 xb}{d}$.
   • One filled with air (or vacuum): Area $(l-x)b$, separation $d$. Capacitance $C_2 = \frac{\epsilon_0 (l-x)b}{d}$.

   The total capacitance $C(x)$ is the sum of these two:

   $C(x) = C_1 + C_2 = \frac{\kappa \epsilon_0 xb}{d} + \frac{\epsilon_0 (l-x)b}{d} = \frac{\epsilon_0 b}{d} [\kappa x + l - x] = \frac{\epsilon_0 b}{d} [(\kappa-1)x + l]$

   Given $\kappa=4$,

   $C(x) = \frac{\epsilon_0 b}{d} [3x + l]$

2. Electric Force on the Dielectric Slab:

   Since the capacitor is connected to a battery, the potential difference $V$ across it is constant. The electric force $F_{electric}$ pulling the dielectric into the capacitor is given by:

   $F_{electric} = \frac{1}{2} V^2 \frac{dC}{dx}$

   First, we find the derivative of capacitance with respect to $x$:

   $\frac{dC}{dx} = \frac{d}{dx} \left( \frac{\epsilon_0 b}{d} [(\kappa-1)x + l] \right) = \frac{\epsilon_0 b}{d} (\kappa-1)$

   Substitute $\kappa=4$:

   $\frac{dC}{dx} = \frac{\epsilon_0 b}{d} (4-1) = \frac{3 \epsilon_0 b}{d}$

   Now, calculate the electric force:

   $F_{electric} = \frac{1}{2} V^2 \left( \frac{3 \epsilon_0 b}{d} \right) = \frac{3 \epsilon_0 b V^2}{2d}$

3. Equilibrium Condition:

   The electric force $F_{electric}$ pulls the dielectric slab into the capacitor. The spring, initially unstretched, gets elongated by $x$ and exerts a restoring force $F_{spring} = kx$ in the opposite direction (pulling the slab out). At equilibrium, these forces balance:

   $F_{electric} = F_{spring}$

   $\frac{3 \epsilon_0 b V^2}{2d} = kx$

4. Elongation in the Spring:

   Solving for $x$, which is the elongation in the spring at equilibrium:

   $x = \frac{3 \epsilon_0 b V^2}{2kd}$

The elongation in the spring at equilibrium of the slab is:

$x = \frac{3 \epsilon_0 b V^2}{2kd}$