Question

A diatomic molecule is made of two masses ${{m}_{1}}$ and ${{m}_{2}}$ which are separated by a distance r. If we calculate its rotational energy by applying Bohr’s rule of angular momentum, its energy will be given by (n is an integer)
A.$\dfrac{{{\left( {{m}_{1}}+{{m}_{2}} \right)}^{2}}{{n}^{2}}{{\hbar }^{2}}}{2{{m}_{1}}^{2}{{m}_{2}}^{2}{{r}^{2}}}$
B. $\dfrac{{{n}^{2}}{{\hbar }^{2}}}{2\left( {{m}_{1}}+{{m}_{2}} \right){{r}^{2}}}$
C.$\dfrac{2{{n}^{2}}{{\hbar }^{2}}}{\left( {{m}_{1}}+{{m}_{2}} \right){{r}^{2}}}$
D.$\dfrac{\left( {{m}_{1}}+{{m}_{2}} \right){{n}^{2}}{{\hbar }^{2}}}{2{{m}_{1}}{{m}_{2}}{{r}^{2}}}$

Answer 1

You could first find the moment of inertia of the given diatomic molecule. Then you could find the angular momentum as per Bohr’s postulate. Then recall the expression for rotational kinetic energy and make necessary changes and then substitute the moment of inertia and the angular momentum from Bohr’s postulate and hence find the answer.
Formula used:
Expressions for angular momentum,
$L=mvr=\dfrac{nh}{2\pi }$
$L=I\omega$
Expression for rotational kinetic energy,
$E=\dfrac{1}{2}I{{\omega }^{2}}$
Expression for moment of inertia,
$I=\sum\limits_{i=1}^{n}{{{m}_{i}}{{r}_{i}}^{2}}$

Complete answer:
In the question we are given a diatomic molecule that is made up of two masses ${{m}_{1}}$ and ${{m}_{2}}$, and they are separated by a distance r. We are asked to find the rotational kinetic energy by applying Bohr’s rule of angular momentum.
As per Bohr’s atomic model, the angular momentum of an electron orbiting around the nucleus is quantized, that is, electrons revolve in those orbits only where the angular momentum of an electron is an integral multiple of $\dfrac{h}{2\pi }$
$L=mvr=\dfrac{nh}{2\pi }$
${{L}^{2}}=\dfrac{{{n}^{2}}{{h}^{2}}}{4{{\pi }^{2}}}$ …………………………………….. (1)
Moment of inertia is the analogue for mass in rotational motion. It is given by the expression,
$I=\sum\limits_{i=1}^{n}{{{m}_{i}}{{r}_{i}}^{2}}$

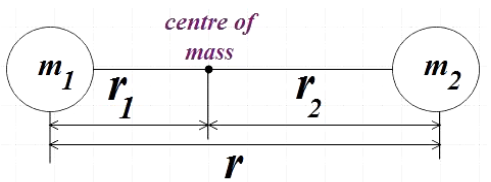
For the given diatomic molecule made of two masses ${{m}_{1}}$ and ${{m}_{2}}$ which are separated by a distance r, the inertia is given by,
$I={{m}_{1}}{{r}_{1}}^{2}+{{m}_{2}}{{r}_{2}}^{2}$ …………………………………. (2)
But we have,
${{m}_{1}}{{r}_{1}}={{m}_{2}}{{r}_{2}}$
$\Rightarrow {{r}_{1}}=\dfrac{{{m}_{2}}{{r}_{2}}}{{{m}_{1}}}$…………….. (3)
But, ${{r}_{1}}+{{r}_{2}}=r$
$\Rightarrow {{r}_{2}}=r-{{r}_{1}}$
Now (3) becomes,
$\Rightarrow {{r}_{1}}=\dfrac{{{m}_{2}}\left( r-{{r}_{1}} \right)}{{{m}_{1}}}=\dfrac{{{m}_{2}}r-{{m}_{2}}{{r}_{1}}}{{{m}_{1}}}$
$\Rightarrow {{m}_{1}}{{r}_{1}}={{m}_{2}}r-{{m}_{2}}{{r}_{1}}$
$\Rightarrow {{r}_{1}}=\dfrac{{{m}_{2}}}{{{m}_{1}}+{{m}_{2}}}r$ ……………………………. (4)
Similarly we can say that,
${{r}_{2}}=\dfrac{{{m}_{1}}}{{{m}_{1}}+{{m}_{2}}}r$ ……………………………… (5)
Substituting (4) and (5) in (2),
$I={{m}_{1}}{{\left( \dfrac{{{m}_{2}}r}{{{m}_{1}}+{{m}_{2}}} \right)}^{2}}+{{m}_{2}}{{\left( \dfrac{{{m}_{1}}r}{{{m}_{1}}+{{m}_{2}}} \right)}^{2}}$
$\Rightarrow I=\dfrac{{{m}_{1}}{{m}_{2}}}{{{m}_{1}}+{{m}_{2}}}{{r}^{2}}$ ……………………………. (6)
But we know that the rotational kinetic energy is given by,
$E=\dfrac{1}{2}I{{\omega }^{2}}$
But we know, $L=I\omega$
$\Rightarrow \omega =\dfrac{L}{I}$
Hence, rotational kinetic energy becomes,
$\Rightarrow E=\dfrac{1}{2}I{{\left( \dfrac{L}{I} \right)}^{2}}=\dfrac{{{L}^{2}}}{2I}$
Substituting for ${{L}^{2}}$ and I from (1) and (6), we get,
$\Rightarrow E=\dfrac{\dfrac{{{n}^{2}}{{h}^{2}}}{4{{\pi }^{2}}}}{2\left( \dfrac{{{m}_{1}}{{m}_{2}}}{{{m}_{1}}+{{m}_{2}}}{{r}^{2}} \right)}$
Let us substitute$\dfrac{h}{2\pi }=\hbar$, now E becomes,
$\Rightarrow E=\dfrac{{{n}^{2}}{{\hbar }^{2}}\left( {{m}_{1}}+{{m}_{2}} \right)}{2{{m}_{1}}{{m}_{2}}{{r}^{2}}}$
Therefore, the rotational kinetic energy of the diatomic molecule is given by,
$E=\dfrac{\left( {{m}_{1}}+{{m}_{2}} \right){{n}^{2}}{{\hbar }^{2}}}{2{{m}_{1}}{{m}_{2}}{{r}^{2}}}$

Hence, the answer to the question is option D.

Note:
For better understanding of the question you could first make a sketch of the system. While deriving such expressions always cross check with the given options and make necessary changes accordingly. Here for example, you could derive the whole set of expressions keeping ${{r}_{1}}$ and ${{r}_{2}}$. But in the above given options, those terms are not there and hence they have to be substituted.