Question
Question: A diatomic molecule is formed by two atoms which may be treated as mass points \(m_1\) and \(m_2\) j...
A diatomic molecule is formed by two atoms which may be treated as mass points m1 and m2 joined by a massless rod of length r. Then, the moment of inertia of the molecule about an axis passing through the center of mass and perpendicular to rod is:
A. Zero
B. (m1+m2)r2
C. (m1m2m1+m2)r2
D. (m1+m2m1m2)r2
Solution
Hint: for this we need to have basic knowledge of center of mass and moment of inertia. Moment of Inertia can be defined as how easily a body can be rotated about a given axis. It is a rotational analogue of mass.
Step by step solution:
1. Let us first draw a figure which will help us in better understanding of the Question.
Below we have drawn a rod AB where m1 is the mass at point A and m2 is the mass at point B. At point O we have assumed the center of mass of the rod. We have drawn a perpendicular axis to the rod about which moment of inertia is to be calculated. Let r1 be the distance between point A and O and r2 be the distance between point B and O.
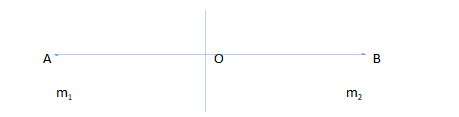
2. As we know that the position of center of mass of the particles is given by
X=m1+m2+.....mnm1x1+m2x2+.......mnxn=∑mi∑mixi …………….equation 1
So here according to our figure we have r1=m1+m2m1×0+m2×r because m1 is at the 0 distance from point A and m2 is at the distance r from point A.
Again r1=m1+m2m2×r ………………equation 2
And r2=r−m1+m2m2×r ……………..equation 3
3. Now Moment of Inertia is given by I=m1x12+m2x22+.........mnxn2
Here in our question I=m1r12+m2r22
With the help of equations 2 and 3 we get
I=(m1+m2)2m1m22r2+(m1+m2)2m12m2r2
Now taking some common terms
I=(m1+m2)2m1m2r2(m1+m2)
After doing the simplifications we get:
I=m1+m2m1m2r2
Or it can also be written as I=(m1+m2m1m2)r2
Hence option D is correct.
Note: In this question basic knowledge of moment of inertia and simple algebra is used. We can also solve this type of question using numerical values instead of variables.
