Question

A diatomic ideal gas is heated at constant volume until the pressure is doubled and again heated at constant pressure until the volume is doubled. Find the average molar heat capacity of the whole process.
A. $\dfrac{{13R}}{6}$
B. $\dfrac{{19R}}{6}$
C. $\dfrac{{23R}}{6}$
D. $\dfrac{{17R}}{6}$

Answer 1

The entire process consists of an isochoric process where the pressure increases and an isobaric process where the volume increases. Thus the heat absorbed for the entire process can be expressed as the sum of the heat absorbed in the isochoric process and the isobaric process. The ideal gas equation gives how the temperature changes for each process.

Formula used:
->The heat gained or lost in any thermodynamic process is given by, $\Delta Q = nC\Delta T$ where $n$ is the number of moles present in the sample, $C$ is the molar specific heat and $\Delta T$ is the change in temperature for the process.
->The ideal gas equation is given by, $PV = nRT$ where $P$ is the pressure of the sample, $V$ is the volume of the sample, $n$ is the number of moles present in the sample, $R$ is the gas constant, $T$ is the temperature of the sample.

Complete step-by-step solution:
Step 1: Sketch a P-V diagram for the whole process.

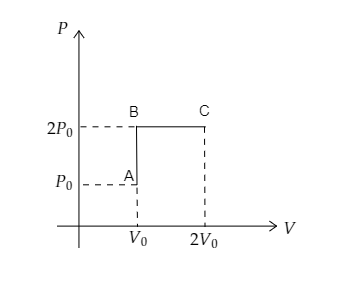
In the above diagram, the path AB refers to the isochoric process where the pressure is doubled and the path BC refers to the isobaric process where the volume is doubled.
We have taken the initial pressure of the gas at A to be ${P_0}$ and the initial volume to be ${V_0}$ .
At B the pressure of the gas will be $P = 2{P_0}$ while the volume remains the same as ${V_0}$.
At C the volume doubles to become $V = 2{V_0}$ while the pressure remains to be $P$ .
Step 2: Use the ideal gas equation to express the change in the temperature for the paths AB and BC.
The ideal gas equation is given by, $PV = nRT$ --------- (1)
For the whole process, the number of moles $n$ present in the sample remains constant.
From equation (1) we know that for the path AB the temperature change is proportional to the change in pressure as the volume remains constant along AB. The temperature doubles.
If ${T_A} = {T_0}$ is the initial pressure at A then at B it will be ${T_B} = 2{T_0}$
$\Rightarrow \Delta {T_{AB}} = {T_B} - {T_A} = 2{T_0} - {T_0} = {T_0}$
For the path BC, as the pressure remains constant the temperature change will be proportional to the change in volume of the gas and so it doubles.
At B the temperature is ${T_B} = 2{T_0}$ so at C it will be ${T_C} = 4{T_0}$ .
$\Rightarrow \Delta {T_{BC}} = {T_C} - {T_B} = 4{T_0} - 2{T_0} = 2{T_0}$
Then the temperature change for the whole process ABC is given by, $\Delta {T_{ABC}} = {T_C} - {T_A}$
Substituting for ${T_C}$ and ${T_A}$ in the above relation we get, $\Delta {T_{ABC}} = 4{T_0} - {T_0} = 3{T_0}$
Step 3: Express the relation for the heat absorbed in the isobaric and isochoric process.
The heat absorbed in the isochoric process is given by, $\Delta {Q_{AB}} = n{C_V}\Delta {T_{AB}}$ -------- (2)
where ${C_V}$ is the molar specific heat at constant volume.
Substituting for ${C_V} = \dfrac{{5R}}{2}$ and $\Delta {T_{AB}} = {T_0}$ in equation (2) we get, $\Delta {Q_{AB}} = n\dfrac{{5R}}{2}{T_0}$
The heat absorbed in the isobaric process is given by, $\Delta {Q_{BC}} = n{C_P}\Delta {T_{BC}}$ -------- (3)
where ${C_P}$ is the molar specific heat at constant pressure.
Substituting for ${C_P} = \dfrac{{7R}}{2}$ and $\Delta {T_{BC}} = 2{T_0}$ in equation (3) we get, $\Delta {Q_{BC}} = n\dfrac{{7R}}{2}2{T_0}$
Thus the heat absorbed during the isochoric process is $\Delta {Q_{AB}} = n\dfrac{{5R}}{2}{T_0}$ and that for the isobaric process is $\Delta {Q_{BC}} = n\dfrac{{7R}}{2}2{T_0}$ .
Step 4: Express the heat absorbed for the whole process ABC to find the average molar specific heat.
The heat absorbed for the whole process ABC is given by, $\Delta {Q_{ABC}} = nC\Delta {T_{ABC}}$ ------- (4)
The heat absorbed for the entire process can also be expressed as $\Delta {Q_{ABC}} = \Delta {Q_{AB}} + \Delta {Q_{BC}}$----- (5)
Combining equations (4) and (5) we get, $nC\Delta {T_{ABC}} = \Delta {Q_{AB}} + \Delta {Q_{BC}}$ ------ (6)
Substituting for $\Delta {T_{ABC}} = 3{T_0}$ , $\Delta {Q_{AB}} = n\dfrac{{5R}}{2}{T_0}$ and $\Delta {Q_{BC}} = n\dfrac{{7R}}{2}2{T_0}$ in equation (6) we get, $nC3{T_0} = n\dfrac{{5R}}{2}{T_0} + n\dfrac{{7R}}{2}2{T_0}$
$\Rightarrow 3C = \dfrac{{5R + 14R}}{2}$
$\Rightarrow C = \dfrac{{19R}}{6}$
Thus the average molar specific heat capacity is obtained as $C = \dfrac{{19R}}{6}$ .
So the correct option is B.

Note:- For an isochoric process, the volume of the system remains constant and for an isobaric process, the pressure remains constant. The ideal gas is said to be diatomic. For a diatomic gas having $f = 5$ degrees of freedom, the molar specific heat at constant volume is given by, ${C_V} = \dfrac{{fR}}{2} = \dfrac{{5R}}{2}$ while the molar specific heat at constant pressure is given by, ${C_V} = \left( {1 + \dfrac{f}{2}} \right)R = \dfrac{{7R}}{2}$