Question

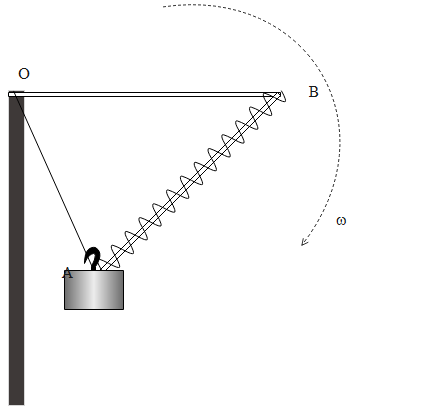
A device (shown in figure) consists of a smooth L-shaped rod located in a horizontal plane and a sleeve A of mass $m$ attached by a weightless spring to a point B. The spring stiffness is equal to k. The whole system rotates with a constant angular velocity $\omega$ about a vertical axis passing through the point O. Find the elongation of the spring. How is the result affected by the rotation direction?

Answer 1

Both centripetal and centrifugal forces in a circular motion are equal in magnitude and opposite in direction. So, the components of normal reaction and spring force, provide centripetal force. Tangential force in circular motion is zero. We use these conditions to obtain expression for change in length.

Formula used:
Centripetal force, ${{F}_{cp}}=m{{\omega }^{2}}r$

Complete step by step answer:
First, we draw the free body diagram of the device. The forces which are acting on the sleeve are; its weight in vertically downward direction, spring force along the length of the spring and normal reaction by the rod perpendicular to its length.

The components of normal reaction and spring force provide the centripetal force required to rotate the system. If $N$ is the normal reaction force and $F$is the spring force then,
$N\sin \theta +F\cos \theta ={{F}_{cp}}=m{{\omega }^{2}}r$ Where $r$ is as shown in the figure.
From diagram, we can note that $r\cos \theta ={{l}_{0}}+\Delta l$
${{l}_{0}}\,\text{and }\Delta l$ is the initial length and the change in length after mass is attached respectively.
Similarly tangential force on the system is zero, since it is moving in uniform circular motion.
$N\cos \theta -F\sin \theta ={{F}_{t}}=0$
$\Rightarrow N=\dfrac{F\sin \theta }{\cos \theta }$
Substituting this value in centripetal force expression, we have
$\dfrac{F\sin \theta }{\cos \theta }.\sin \theta +F\cos \theta =m{{\omega }^{2}}\left( \dfrac{{{l}_{0}}+\Delta l}{\cos \theta } \right)$
Since spring force, $F=k\Delta l$. Substituting this value, we get
$k\Delta l\left( \dfrac{{{\sin }^{2}}\theta }{\cos \theta }+\cos \theta \right)=m{{\omega }^{2}}\left( \dfrac{{{l}_{0}}+\Delta l}{\cos \theta } \right)$
$\Rightarrow k\Delta l\left( \dfrac{{{\sin }^{2}}\theta +{{\cos }^{2}}\theta }{\cos \theta } \right)=m{{\omega }^{2}}\left( \dfrac{{{l}_{0}}+\Delta l}{\cos \theta } \right)$
$\Rightarrow \dfrac{k\Delta l}{\cos \theta }=m{{\omega }^{2}}\left( \dfrac{{{l}_{0}}+\Delta l}{\cos \theta } \right)(\because {{\sin }^{2}}\theta +co{{s}^{2}}\theta =1)$
On rearranging and solving this for $\Delta l$, we get
$\Delta l=\dfrac{m{{\omega }^{2}}{{l}_{0}}}{k-m{{\omega }^{2}}}=\dfrac{{{l}_{0}}}{\left( \dfrac{k}{m{{\omega }^{2}}}-1 \right)}$
We may note that elongation in spring $\Delta l$ is independent of direction of rotation.

Note:
The centripetal force is directed at right angles to the direction of motion and is always along the radius and towards the centre of the circular path.In circular motion, tangential force is always zero, since there is no linear movement of the object.