Question

A) Describe briefly how a diffraction pattern is obtained on a screen due to a single narrow slit illuminated by a monochromatic source of light. Hence obtain the conditions for the angular width of secondary maxima and secondary minima.
B) Two wavelengths of sodium light $590nm$ and $596nm$ are used in turn to study the diffraction taking place at a single slit of aperture $2 \times {10^{ - 6}}m$ . The distance between the slit and the screen is $1.5m$ . Calculate the separation between the positions of the first maxima and the diffraction pattern obtained in the two cases.

Answer 1

The intensity of any point on the screen on which a light, passed through a slit, hits depends on the path difference between the waves arising from different parts of the wave-front at the slit. At the center, intensity will be the maximum.

Complete step by step solution:
A) We know, diffraction is the phenomenon of change in the direction of light around the sharp corners of an obstacle and spreading into the regions of geometrical shadow.

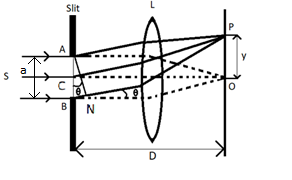From the diagram, we can find the approximate path different and is given by, $BN = AB\sin \theta = a\sin \theta$
For the path difference, $Bn = n\lambda$ constructive interference, happens,
Then, $n\lambda = a\sin {\theta _n}$
$\Rightarrow \dfrac{{n\lambda }}{a} = \sin {\theta _n}$
And this expression is called the ${n^{th}}$ Bright Fringe.
We know $\tan {\theta _n} = \dfrac{{{y_n}}}{D}$
But, the value of ${\theta _n}$ is lower, the value of $\tan {\theta _n}$ will be approximately equal to $\sin {\theta _n}$ ;
That is, $\sin {\theta _n} \approx \tan {\theta _n}$
Substituting the values of both $\sin {\theta _n}$and$\tan {\theta _n}$ , we get,
$\dfrac{{{y_n}}}{D} = \dfrac{{n\lambda }}{a}$
$\Rightarrow {y_n} = \dfrac{{n\lambda D}}{a}$
Width of the secondary maxima is given by the equation,
$\beta = {y_n} - {y_{n - 1}}$
$= \dfrac{{nD\lambda }}{a} - \dfrac{{(n - 1)D\lambda }}{a}$
That is, $\beta = \dfrac{{\lambda D}}{a}$
Width of the secondary minima is given by the equation,
${\beta’} = \dfrac{{nD\lambda }}{a} - \dfrac{{(n - 1)D\lambda }}{a}$
That is, ${\beta’} = \dfrac{{\lambda D}}{a}$
Angular width is independent of n; therefore all secondary minima and maxima have the same width. At the central point c Angle is zero, and hence, all the parts of the slit are in phase. Because of this, at point C, intensity is maximum.

B) Let’s define all the data given in the question,
The given two wavelengths are
${\lambda _1} = 590nm$
${\lambda _2} = 596nm$
Slit of aperture$= 2 \times {10^{ - 6}}m$.
The distance between the slit and the screen= $1.5m$
The linear separation between the first minima of the two wavelength on the screen will be equal to,
$\dfrac{{3({\lambda _2} - {\lambda _1})}}{a} \times D$
Therefore the separation will be equal to
= \dfrac{{3(596 - 590)}}{{2 \times {{10}^{ - 6}}}} \times 1.5 \\\ \\\
$= 13.5 \times {10^{ - 3}}m$
$= 13.5mm$
That is, separation between the positions of the first maxima and the diffraction pattern obtained in the two cases will be equal to $13.5mm$.

Note: When a monochromatic light is passed through a slit, the diffraction pattern is obtained on the screen placed to the light. In the centre, brightness will be higher and this portion is called the central maximum.