Question

(a) Derive the expression for the torque on a rectangular current carrying loop suspended in a uniform magnetic field.
(b) A proton and a deuteron having equal moments enter a region of a uniform magnetic field at right angle to the direction of a field. Depict their trajectories in the field.

Answer 1

Hint: Before attempting this question, you should have prior knowledge of the effect on rectangular current carrying loops when brought under the effect of uniform magnetic field. Also remember to construct the diagram before moving to a solution using the diagram will help you to approach towards the solution.

Complete step-by-step answer:
(a)


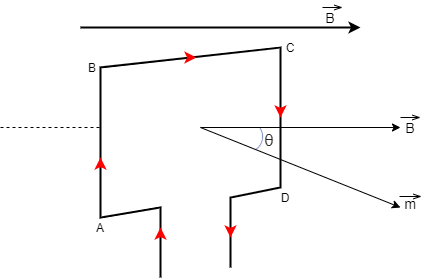
First, let the rectangular carrying loop be align such that its magnetic moment in vector form will be $\overrightarrow m$ , and let the uniform magnetic field be $\overrightarrow E$ such that $\overrightarrow m$ makes and angle $\theta$ with $\overrightarrow E$ Now, let’s find out the force acting on the loop
Let us consider that there are two sides AD and BC and we know that according to Fleming’s left hand rule, the magnetic fields on the sides are equal and opposite which means the force on AD and BC are equal and opposite, thus they cancel each other
Let us take forces on thus two arms BC and AD be ${F_{BC}}$ and ${F_{AD}}$ , as the sides are equal and opposite so the forces AB and CD are also equal and opposite but the forces AB and CD are not collinear which means they are not in a single straight line know as axis and when they are collinear they form couple which means the pair of force are equal in magnitude but their direction is opposite, in other words two equal and opposite forces whose lines of actions are not same
Due to this a force which is known as torque and torque can be given as $F \times$ perpendicular distance.
So, here torque will be $\tau = {F_{AB}}.\dfrac{e}{2}\sin \theta + {F_{CD}}.\dfrac{e}{2}\sin \theta$
Here, the perpendicular distance is $\dfrac{e}{2}\sin \theta$ .
Since, we know that force on AB i.e. ${F_{AB}}$ and force on CD i.e. ${F_{CD}}$ is equal which can be written as $\left| {{F_{AB}}} \right| = \left| {{F_{CD}}} \right| = E \times I \times l$
We know that $Force = q \times E$and here, q is I so F=EI
Now, $\tau = EIl \times b\sin \theta$
$\tau = EI(lb)\sin \theta$
$\Rightarrow$ $EI \times A\sin \theta$
Here, we know that area of rectangle is $l \times b$
Since, the magnetic moment m = $I\left| A \right|$
So, $\tau = mE\sin \theta$
And in vector form we can write as: $\overrightarrow \tau = \overrightarrow m \times \overrightarrow E$

(b)
According to the question the proton and deuteron enters the magnetic field at right angle, it follows a circular motion because when $\theta = {90^ \circ }$ , the force acting on the following particle is maximum and the direction is perpendicular to the path of the particle, the force acting on the particle is centripetal force which results in the circulation motion of particle.
Hence, it follows a circular trajectory.

Note: In the above solution we came across the concept of magnetic field which can be defined as the field of force generated by a magnetic material or any current carrying body under which any secondary body gets influenced by the magnetic force. Generally the effect of magnetic field generated by the magnetic material is very less so to generate a strong magnetic field we use the electro magnet which is formed by passing the electric current from the coil, larger the current the stronger the magnetic field becomes.