Question

(a) Derive a relation for electric field due to an electric dipole at a point on the equatorial plane of the electric dipole. Draw necessary diagrams.
(b) An electric dipole of charge ±1 AC exists inside a spherical Gaussian surface of radius 1cm. Write the value of outgoing flux from the Gaussian surface.
(c) Potential on the surface of a charged spherical shell of radius 10cm is 10V. Write the value of potential at 5cm from its centre.

Answer 1

Hint: This question belongs to electric dipole. We will be dealing with three different cases. As the case one states the basic diagram to see the Electric field at point P due to each charge of dipole, by placing the required formula and keeping the basic values from it will help to find the basic answer, where if we look at the case two we need to know the Total charge enclosed by the spherical Gaussian surface, by finding the outgoing flux we can find the answer. In case three, we can see the magnitude of potential at a point inside the charged spherical shell by finding potential at the surface, we can find the required data.

Complete step-by-step answer:
Case one-

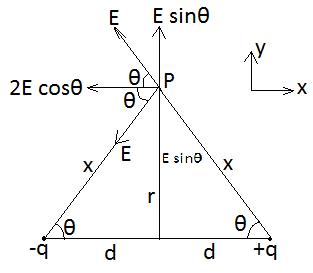
The electric field at point P due to each charge of dipole is shown in the figure.
$\Rightarrow E = \dfrac{{kq}}{{{x^2}}}$
From the figure we can see that $x = \sqrt {{d^2} + {r^2}}$
So, $E = \dfrac{{kq}}{{{d^2} + {r^2}}}$
Now the Electric field component at P in y direction ${E_Y} = E\sin \theta - E\sin \theta = 0$.
So, the Electric field component at P in x direction ${E_x} = - 2E\cos \theta$ where$\Rightarrow \theta = \dfrac{d}{x} = \dfrac{d}{{\sqrt {{d^2} + {r^2}} }}$
We will get -
$\Rightarrow {E_x} = \dfrac{{ - 2kqd}}{{{{\left( {{d^2} + {r^2}} \right)}^{\dfrac{3}{2}}}}}$
The Dipole moment of dipole at point P = q(2d)
Hence, the electric field at the point P will be–
$\Rightarrow {E_p} = {E_x} = \dfrac{{ - kP}}{{{{\left( {{d^2} + {r^2}} \right)}^{\dfrac{3}{2}}}}}$
The negative sign present above shows that the electric field at a point in an equatorial plane always points in a direction opposite to that of the electric dipole moment.

Case two-
We need to find the value of outgoing flux from the Gaussian surface
As we know that Total charge enclosed by the spherical Gaussian surface ${q_{enc}}$
$\Rightarrow {q_{enc}} = 1\mu C - 1\mu C = 0$
Hence the outgoing flux $\phi$ would be
$\Rightarrow \phi = \dfrac{{{q_{enc}}}}{{{\varepsilon _0}}} = 0$

Case three-
We need to find the value of potential at 5cm from its center.
We know that the magnitude of potential at a point inside the charged spherical shell is equal to that at its surface because the electric field inside that spherical shell is zero.
So, the Potential at the surface ${V_s}$ would be 10 V (given in the question)
Hence the potential at a point 5cm from its center $V' = {V_S} = 10V$
Therefore, the value of potential at 5cm from its center is 10V.

Note- Electric field, an electric property connected to each charge point in space, whenever the charge is present in any shape. The magnitude and direction of the electric field is conveyed by the value of E, or precisely the electric field or electric field force.