Question
Question: (a) Define the optical centre of a spherical lens. (b) A diverging lens has a focal length of \(2...
(a) Define the optical centre of a spherical lens.
(b) A diverging lens has a focal length of 20 cm. At what distance should an object of height 4 cm from the optical centre of the lens be placed so that its image is formed 10 cm away from the lens. Find the size of the image also.
Solution
A diverging lens is a concave lens. The refraction of light rays as they pass through the lens determines how well the lens works. When light rays enter a concave lens, they diverge, causing the lens to behave like a diverging lens. By the help of the Mirror Formula calculate the object distance after calculating Object distance Take out the magnification of the object.
Formula used:
By lens Formula -
f1=v1−u1
Size of the image - hi=uvh0
Complete step-by-step solution:
a) Optical centre is the point lying on the principal axis of a lens through which light passes through without undergoing any deviation.
b) Given
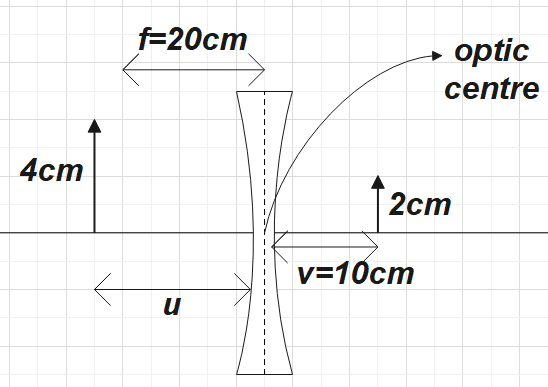
Focal length, f=−20 cm
Height of the object, h1=4 cm
Image distance, v=−10 cm
To find: Object distance =? Size of the image, h2= ?
Now, using the lens formula,
f1=v1−u1
=−10−1−−201
=10−1+201
=20−2+1
u=−20 cm
Therefore, the object is at a distance of 20 cm on the left side of the lens.
Size of the image is given by,
hi=uvh0
=−20−10×4
=2 cm
Size of the object is =2 cm
Note: A converging lens is usually followed by a diverging lens, which is then followed by another converging lens. By moving toward or away from the object, the first lens adjusts the magnification level of the image. The inverted image is flipped by passing light through the first lens and the diverging lens. After refraction through the concave lens, a ray of light that is parallel to the principal axis diverges, and when we produce these rays backward, they appear to meet at a point called focus. Because the lens diverges the ray of light, it is called a diverging lens.
