Question

(a). Define streamline
(b). Write any two properties of streamlines
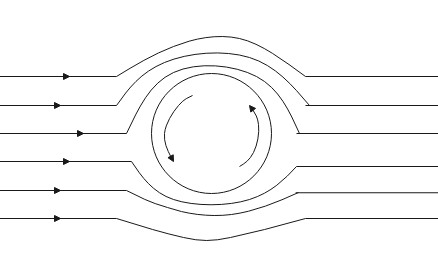
(c). Draw streamlines for clockwise spinning spheres
(d). Derive equation of continuity

Answer 1

Streamline is a path followed by imaginary particles in a fluid. The streamlines give us the direction of flow of the fluid. For clockwise spinning circles, the streamlines around them show us the motion of fluid around it. The equation of continuity gives us the relation between the area, density and velocity of a fluid flowing through a body of variable area of cross section.

Formula used:
$\omega ={{\omega }_{0}}+\alpha t$
${{\omega }^{2}}=\omega _{0}^{2}+2\alpha \theta$

Complete step by step solution:
(a). Streamlines can be defined as the path taken by imaginary particles that are flowing along with the fluid. In a steady flow, the streamlines are constant.
(b). Two properties of streamlines are-
Tangent drawn to streamlines gives the direction of the velocity of fluid at that point
When the streamlines are crowded together, the fluid is flowing at high speeds whereas where the streamlines are far away from each other, the flow of the fluid is slow.
(c). The streamlines for clockwise spinning spheres are given in the figure given below


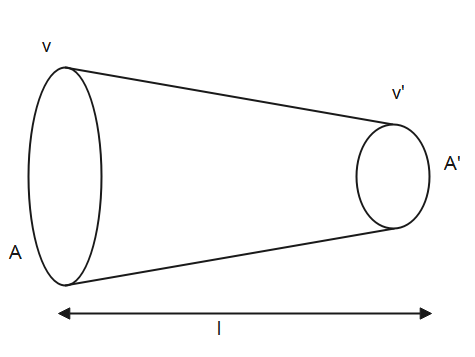
(d). Let us assume that the fluid flowing through the above pipe for a short interval of time, $\Delta t$.
If the fluid covers a distance of $\Delta {{x}_{1}}$ at the lower end of the pipe flowing with velocity, $v$, then the value of $\Delta {{x}_{1}}$ will be-
$\Delta {{x}_{1}}=v\Delta t$
The volume of the fluid will be-
Volume= area x length
$\begin{aligned} & V=A\Delta {{x}_{1}} \\\ & \Rightarrow V=Av\Delta t \\\ \end{aligned}$
Therefore, the volume of the fluid flowing in time interval $\Delta t$ is $Av\Delta t$.
We know that,
$\begin{aligned} & \rho =\dfrac{m}{V} \\\ & \Rightarrow m=\rho V \\\ \end{aligned}$
Here, $\rho$ is the density of the fluid
$m$ is the mass of the fluid
$V$ is the volume of the fluid
Therefore, from the above equation, the mass of the fluid will be-
$\begin{aligned} & m=\rho V \\\ & \Rightarrow m=\rho Av\Delta t \\\ \end{aligned}$
Therefore, the mass of the fluid is $\rho Av\Delta t$.
The mass flux is the mass of the fluid passing per unit time through an area of cross section. The mass flux for the fluid flowing through the lower end of the pipe will be-
$\dfrac{m}{\Delta t}={{\rho }_{1}}Av$ - (1)
Similarly, the mass flux for the fluid flowing through the upper end of the pipe will be
$\dfrac{m'}{\Delta t}={{\rho }_{2}}A'v'$ - (2)
Since the same fluid flows through both ends of the pipe, the density is constant. Hence, the mass flux flowing through the lower end and upper end of the pipe is the same. Therefore from eq (1) and eq (2), we get,
${{\rho }_{1}}Av={{\rho }_{2}}A'v'$
So we can say that, $\rho Av=\text{constant}$
Hence the equation of continuity is verified.

Note: The mass and time both are constant; hence, the mass flux is constant. The volume flow rate is the product of area and velocity and it is also conserved for a fluid flowing through a pipe with variable area of cross section. The fluid is incompressible, so the density at both ends will be the same.