Question

(a) Deduce the expression for the torque acting on a dipole of dipole moment $\overrightarrow{p}$ in the presence of a uniform electric field $\overrightarrow{E}$.
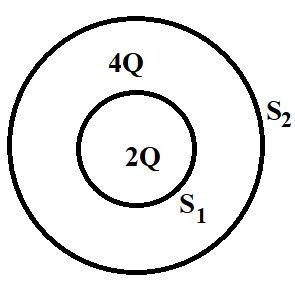
(b) Consider two hollow concentric spheres, ${{S}_{1}}$ and ${{S}_{2}}$, enclosing charges $2Q$ and $4Q$ respectively, as shown in the figure.

1. Find out the ratio of electric flux through them.
2. How will the electric flux through the sphere ${{S}_{1}}$ change if a medium of dielectric constant $'{{\varepsilon }_{r}}'$ is introduced in the space inside ${{S}_{1}}$, in place of air? Deduce necessary expression.

Answer 1

(a) Even though the net force acting on a dipole in a uniform electric field is zero, the forces on each end of the dipole, together form a couple. Torque acting on a dipole is nothing but the moment of the couple, formed by the forces acting on each end of the dipole.
(b) Electric flux through a closed surface kept in free space is given by Gauss’s theorem. When the sphere is kept in a dielectric medium, there is a slight change in the formula given by Gauss’s theorem.

Formula used:
(a)
$1)\left| \overrightarrow{p} \right|=q\times 2a$
$2)F=qE$
$3)\overrightarrow{\tau }=\overrightarrow{p}\times \overrightarrow{E}$
(b)
${{\phi }_{E}}=\dfrac{Q}{{{\varepsilon }_{0}}}$

Complete answer:
(a)
Let us consider a dipole of dipole moment $\overrightarrow{p}$, in the presence of a uniform electric field $\overrightarrow{E}$, as shown in the following figure. Point $A$ of the dipole has a charge $-q$ and point $B$ of the dipole has a charge $+q$. Length between these two charges is $2a$. Also, from the figure, it is clear that the angle between the dipole and the electric field is given by $\theta$. Dipole moment of the dipole is equal to the product of charge on each end of the dipole and the distance between these charges. This dipole moment acts in the direction from point $A$ to point $B$. Mathematically, magnitude of dipole moment is given by
$\left| \overrightarrow{p} \right|=q\times 2a$
where
$\overrightarrow{p}$ is the dipole moment of the dipole
$q$ is the charge on each end of the dipole
$2a$ is the length of the dipole
Let this be equation 1.

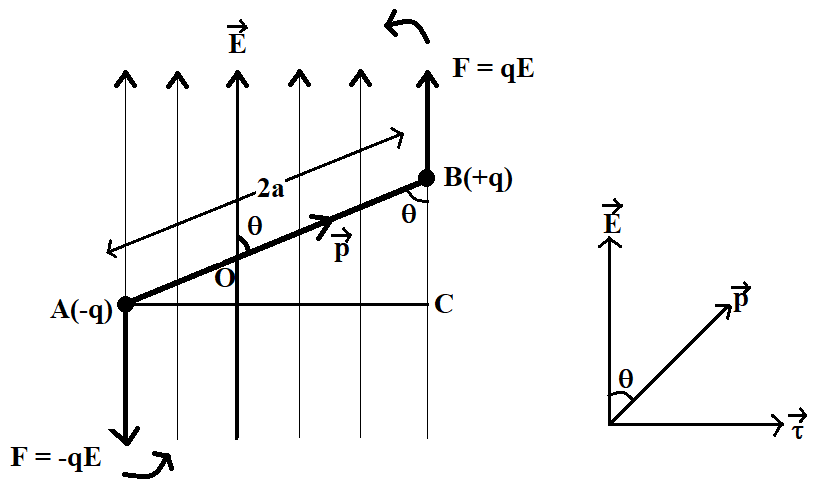
Now, when the dipole is kept in a uniform electric field, the charges on both ends of the dipole experience a force due to the electric field. Force on charge $+q$ as well as $-q$ is given by
$F=qE$
where
$F$ is the magnitude of force acting on each charge of the dipole
$q$ is the magnitude of each charge of the dipole
$E$ is the magnitude of electric field
Let this be equation 2.
It is important to note that the force acting on charge $+q$ is along the direction of the electric field whereas the force acting on charge $-q$ is in a direction opposite to the direction of the electric field. Therefore, the net force acting on the dipole due to the electric field is given by
${{F}_{net}}=qE-qE=0$
Thus, it is clear that the electric field does not create a force on the dipole.
However, as the forces acting on each charge of the dipole are equal, unlike and parallel, acting at different points, they form a couple. This couple tends to rotate the dipole in anticlockwise direction, as shown in the figure. Hence, the couple tends to align the dipole, along the direction of the electric field.
We know that a couple is a pair of equal forces, oppositely directed and displaced by perpendicular distance between the forces. Therefore, if we draw $AC$ perpendicular to the electric field as shown in the figure, $AC$ becomes the arm of the couple. Clearly, $AC$ is given by
$AC=AB\sin \theta =2a\sin \theta$
where
$AC$ is the arm of the couple
$AB=2a$ is the length of the dipole
$\theta$ is the angle between the dipole and the electric field
Let this be equation 3.
Torque acting on a dipole can be defined as the moment of a couple formed by the forces on each end of the dipole. Moment of a couple is nothing but the product of force and the arm of the couple. Mathematically, torque can be represented as
$\tau =F\times AC$
where
$\tau$ is the torque acting on the dipole
$F$ is the magnitude of force acting on each charge of the dipole
$AC$ is the arm of the couple formed by the forces on each end of the dipole
Let this be equation 4.
Substituting equation 1, equation 2 and equation 3 in equation 4, we have
$\tau =F\times AC=qE\times 2a\sin \theta =pE\sin \theta$
where
$\tau$ is the torque acting on the dipole
$p$ is the magnitude of dipole moment of the dipole
$E$ is the magnitude of the electric field
$\theta$ is the angle between the dipole and the electric field
Let this be equation 5.
Equation 5 can also be written in vector form as given below.
$\overrightarrow{\tau }=\overrightarrow{p}\times \overrightarrow{E}$
Hence, the above explanation gives the derivation of torque acting on a dipole in a uniform electric field.

(b)
Electric flux over an area of electric field is the nothing but the number of electric field lines crossing this area. Electric flux of a closed surface containing charge inside, is given by Gauss’s theorem. Gauss’s theorem states that the total electric flux over a closed surface in vacuum is $\dfrac{1}{{{\varepsilon }_{0}}}$ times the total charge, contained inside the closed surface. Mathematically, Gauss’s theorem is represented by
${{\phi }_{E}}=\dfrac{Q}{{{\varepsilon }_{0}}}$
where
${{\phi }_{E}}$ is the total electric flux over a closed surface
$Q$ is the charge inside the closed surface
${{\varepsilon }_{0}}$ is the electric permeability of free space
Let this be equation 1.

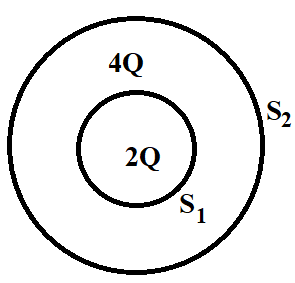
Coming to the question, we are provided with two hollow concentric spheres ${{S}_{1}}$ and ${{S}_{2}}$, enclosing charges $2Q$ and $4Q$ respectively, as shown in the figure below. We are required to find the ratio of electric flux through them.

Applying Gauss’s theorem to sphere ${{S}_{1}}$, we have
${{\phi }_{E}}({{S}_{1}})=\dfrac{2Q}{{{\varepsilon }_{0}}}$
where
${{\phi }_{E}}({{S}_{1}})$ is the total electric flux over the sphere ${{S}_{1}}$
$2Q$ is the charge inside ${{S}_{1}}$
${{\varepsilon }_{0}}$ is the electric permeability of free space
Let this be equation 2.

Applying Gauss’s theorem to sphere ${{S}_{2}}$, we have
${{\phi }_{E}}({{S}_{2}})=\dfrac{4Q}{{{\varepsilon }_{0}}}$
where
${{\phi }_{E}}({{S}_{2}})$ is the total electric flux over the sphere ${{S}_{2}}$
$4Q$ is the charge inside ${{S}_{2}}$
${{\varepsilon }_{0}}$ is the electric permeability of free space
Let this be equation 3.

Taking the ratio of equation 2 and equation 3, we have
$\dfrac{{{\phi }_{E}}({{S}_{1}})}{{{\phi }_{E}}({{S}_{2}})}=\dfrac{\dfrac{2Q}{{{\varepsilon }_{0}}}}{\dfrac{4Q}{{{\varepsilon }_{0}}}}=\dfrac{1}{2}$
Therefore, the ratio of electric flux through ${{S}_{1}}$ and ${{S}_{2}}$ is $1:2$
Coming to the last part of the question, we are required to deduce an expression for the electric flux of ${{S}_{1}}$, if the medium inside ${{S}_{1}}$ is filled with a dielectric of dielectric constant ${{\varepsilon }_{r}}$.
We know that electric permeability of a dielectric medium is equal to the product of electric permeability of free space and dielectric constant of the dielectric medium, as given below.
$\varepsilon ={{\varepsilon }_{r}}{{\varepsilon }_{0}}$
where
$\varepsilon$ is the electric permeability of a dielectric medium
${{\varepsilon }_{r}}$ is the dielectric constant of the dielectric medium
${{\varepsilon }_{0}}$ is the electric permeability of free space
Let this be equation 4.
Applying equation 4 in equation 2, we have
${{\phi }_{E}}'({{S}_{1}})=\dfrac{2Q}{{{\varepsilon }_{r}}{{\varepsilon }_{0}}}=\dfrac{2Q}{\varepsilon }$
where
${{\phi }_{E}}'({{S}_{1}})$ is the electric flux of the sphere ${{S}_{1}}$, when filled with a dielectric medium of dielectric constant ${{\varepsilon }_{r}}$
$2Q$ is the charge contained inside ${{S}_{1}}$
$\varepsilon$ is the electric permeability of the given dielectric medium

Therefore, when a dielectric medium of dielectric constant ${{\varepsilon }_{r}}$ is filled inside a sphere, the electric flux becomes equal to $\dfrac{1}{\varepsilon }$ times the total charge contained inside the sphere.

Note:
(a) Torque is defined as the rotational equivalent of linear force. If we consider a rigid body connected to a fixed point using a lever arm, the linear force we apply to the fixed point will rotate the rigid body. This rotation is said to be caused by the torque acting on the rigid body. Magnitude of torque is dependent on the force applied, the lever arm and the angle between the force and the lever arm, as follows:
$\tau =F\times$lever arm$\times \sin \theta$
This explanation can be used to deduce equation 4 in solution (a).

(b) It is clear from Gauss’s theorem that electric flux is dependent on the charge inside a closed surface. Therefore, when there is no charge inside a closed surface, the electric flux over the surface of the closed surface too, turns out to be zero. This is given by
$Q=0\Rightarrow {{\phi }_{E}}=0$