Question
Question: (a) Deduce the expression for the potential energy of a system of two charges \({q_1}\) and \({q_2}\...
(a) Deduce the expression for the potential energy of a system of two charges q1 and q2 located r1 and r2, respectively, in an external electric field.
(b) Three point charges, +Q +2Q and −3Q are placed at the vertices of an equilateral triangle ABC of side I. If these charges are displaced to the midpoint A1, B1 and C1, respectively, find the amount of the work done in shifting the charges to the new locations.
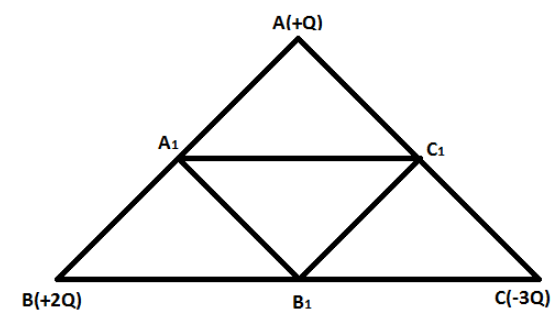
Solution
In this question, we need to first deduce the potential energy of a system which contains two charges of different magnitude and then, evaluate the amount of the work done in shifting the charges to the new locations such that three point charges moved from vertex to mid-point of an equilateral triangle. For this, we will use the generalised formula of the potential energy and substitute the value of the three different charges.
Complete step by step answer:
(a)Firstly, the work done to bring a charge q in the electric field at a distance is given by r1=q1V(r1).
Similarly, the work done to bring a charge q in the electric field at a distance is given by r2=q2V(r2).
Also, the work done on q2 to move it against the force of q1=r12Kq1q2.
Therefore, we can conclude that the potential energy of the system can be given by
q1V(r1)+q2V(r2)+r12Kq1q2.
(b)The work done in moving the charges is equal to the difference between the potential of the initial position and the potential of the final position.
This can be technically written as,
Work done in moving charges = Potential of the Initial position − Potential of the Final position
Now, the potential of the initial system is equal to,
W = {V_{12}} + {V_{23}} + {V_{31}} \\\
\Rightarrow W = 2K{Q^2} + ( - 3K{Q^2}) + ( - 6K{Q^2}) \\\
\Rightarrow W = - 7K{Q^2}J \\\
Now, let us calculate the final potential, that is, the potential after moving to the positions A1, B1 and C1.
V = \dfrac{{K(2Q)(Q)}}{{\left( {\dfrac{1}{2}} \right)}} + \dfrac{{K(Q)( - 3Q)}}{{\left( {\dfrac{1}{2}} \right)}} + \dfrac{{K( - 3Q)(2Q)}}{{\left( {\dfrac{1}{2}} \right)}} \\\
\Rightarrow V = 4K{Q^2} - 6K{Q^2} - 12K{Q^2} \\\
\Rightarrow V = - 14K{Q^2}J \\\
Therefore, the work done can be given by,
Work done = potential of the initial position − potential of the final position
W=−7Q2K−(−14KQ2) ∴W=7KQ2J
So, we can conclude that the amount of the work done in shifting the charges to the new locations is 7KQ2J.
Note: Students get confused when calculating the work done. Instead of finding the difference between the potential of the initial position and the potential of the final position, students tend to add these values. The work done in moving the charges is equal to the difference between the potential of the initial position and the potential of the final position.
