Question

A) Deduce an expression for the frequency of revolution of a charged particle in a magnetic field and show that it is independent of velocity or energy of the particle.
B) Draw a schematic sketch of a cyclotron. Explain giving the essential details of its construction, how it is used to accelerate the charged particle.

Answer 1

When a charged particle revolves in a circular path in uniform a magnetic field, there exists a centripetal force acting on the particle and it will be equal to the magnetic force acting on the particle

Complete step by step solution:
A) The magnetic force acting on a charged particle which is a magnetic field is given by the formula,
Magnetic force, $F = qvB$
Where, $q$ =the charge of the particle
$v$ =velocity of the particle
$B$ =Magnetic field
We know, since the motion is in circular path centripetal force is there, and the force of attraction will be equal to the centripetal force.
$centripetal{\text{ }}force = \dfrac{{m{v^2}}}{r}$
Equating the centripetal force and the magnetic force, we get,
$\Rightarrow \dfrac{v}{r} = \dfrac{{qB}}{m}$
We know frequency is given by,
$f = \dfrac{v}{{2\pi r}} = \dfrac{{qB}}{{2\pi m}}$
That is, $f = \dfrac{{qB}}{{2\pi m}}$
From this equation, it is understood that frequency of revolution of a charged particle in a magnetic field is independent of velocity or energy of the particle.

B) Explanation: Let’s discuss cyclotron; Cyclotron is a device which accelerates particles to very high speeds and it was invented by Ernest O.Lawrence in 1929–1930. A high frequency alternating voltage is used in a cyclotron to accelerate a charged particle. Voltage is applied between two hollow “D”-shaped sheet metal electrodes inside a vacuum chamber. These are represented as D1 and D2 in the figure and collectively known as the “dees”.

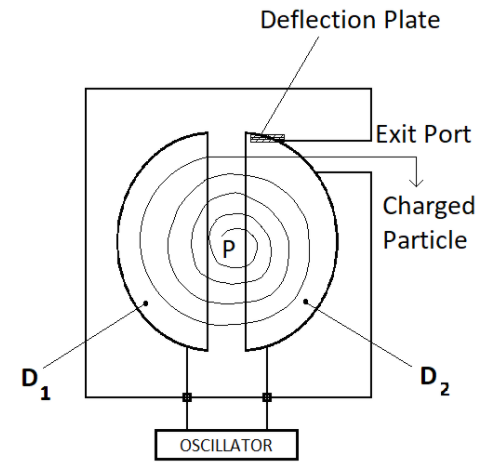
Schematic diagram of a cyclotron is shown in the figure.
The cyclotron is made up of two hollow semi-circular discs. Crossed electric and magnetic fields are used in cyclotrons. An oscillator having adjustable frequency provides the electric field. The forces acting on the particle are centripetal force which is caused by the magnetic field and an accelerating force caused by the electric field.
By adjusting the frequency of the field, equals the frequency of the charged particle, the charged particle accelerates every time and thus the radius gets increased. Finally getting out with a high velocity through the exit port

Note: Radius of a particle in the cyclotron is given by the equation,
Radius, $r = \dfrac{{mv}}{{qB}}$
Where, $B =$ Mass of the particle
$v =$ Velocity of the particle
$q =$ Charge of the particle
$B =$ Magnetic field