Question

A decorative block shown in figure, it is made of two solids, a cube and a hemisphere. The base of the clock is a cube with an edge 5cm and the hemisphere fixed on the top has a diameter of 4.2cm. Find the total surface area of the block. (Take, $\pi =\dfrac{22}{7}$)

Answer 1

Hint:Total surface area of the block will be the surface area of the cube with the surface area of the hemisphere. Subtract the base area of the hemisphere from total surface area to avoid doubling of area.

Complete step-by-step answer:

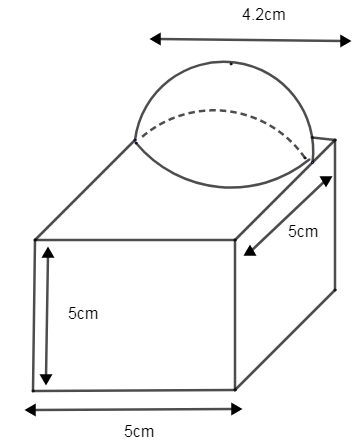
From the figure you can understand that the two solids are a cube and hemisphere. The hemisphere is placed on top of the cube.
Thus we need to find the total surface area of the block. Here the base of the hemisphere is on top of the cube. So it becomes double if we calculate both. Thus we need to subtract the base area of the hemisphere. Thus we can say that the total surface area of the block is the sum of areas of the cube and hemisphere, minus the area of the base of hemisphere.
$\therefore$ Total surface area of block
= Total surface area of cube + curved surface area of hemisphere – base area of hemisphere - (1)
Now let us first find the area of the cube.
Given that the side of cube = 5cm
Thus total surface area of cube $=6\times {{\left( side \right)}^{2}}$
$\begin{aligned} & =6\times {{\left( 5 \right)}^{2}} \\\ & =6\times 5\times 5=150c{{m}^{2}} \\\ \end{aligned}$
$\therefore$ Total surface area of cube = $150c{{m}^{2}}-(2)$
Let us find the curved surface area of the hemisphere.
Given diameter of hemisphere = 4.2cm
Thus radius, $r = \dfrac{diameter}{2}$ = $\dfrac{4.2}{2}=2.1$ cm
We know that,
Curved surface area of hemisphere = $2\pi {{r}^{2}}$
$\begin{aligned} & =2\times \dfrac{22}{7}\times {{\left( 2.1 \right)}^{2}} \\\ & =2\times \dfrac{22}{7}\times 2.1\times 2.1=44\times 0.3\times 2.1 \\\ & =27.72c{{m}^{2}} \\\ \end{aligned}$
$\therefore$ Curved surface area of hemisphere = $27.72c{{m}^{2}}-(3)$
Now base area of hemisphere,
Base of the hemisphere is a circle with radius 2.1 cm.
$\therefore$ Base area of hemisphere = area of circle = $\pi {{r}^{2}}$
$\begin{aligned} & =\dfrac{22}{7}\times 2.1\times 2.1=22\times 0.3\times 2.1 \\\ & =13.86c{{m}^{2}} \\\ \end{aligned}$
$\therefore$ Base area of hemisphere $=13.86c{{m}^{2}}-(4)$
Thus substitute the values of (2), (3) and (4) in equation (1).
$\therefore$ Total surface area of block =
Total surface area of cube + curved surface area of hemisphere – base area of hemisphere.
$\therefore$Total surface area of block = 150 + 27.72 – 13.86 = $163.86c{{m}^{2}}$
Thus we got the total surface area of the block as $163.86c{{m}^{2}}$.

Note: There are few points that you need to remember while solving this question. The base area of the hemisphere should be subtracted from the total surface area of the block. Or else the area gets repeated as the hemisphere is placed on top of the cube. And remember that the base of a cube is a circle.