Question

A dc main supply of emf 220V is connected to a storage battery of emf $200{\text{V}}$ through a resistance of $1\Omega$. The battery terminals are connected to an external resistance $R$. Find the minimum value of $R$ so that a current passes through the battery to charge it.
A) $7\Omega$
B) $9\Omega$
C) $11\Omega$
D) Zero

Answer 1

The voltage across the circuit will be the sum of the emf of the battery and the potential drop across its internal resistance. This will give us the current in the circuit. Here the internal resistance of the storage battery and the external resistance constitute a series connection and so same current will flow through the external resistance. The minimum resistance can then be obtained using Ohm’s law.

Formulas used:
Ohm’s law gives the resistance offered by the circuit as $R = \dfrac{V}{I}$ where $I$ is the current in the circuit and $V$ is the potential difference across the circuit.
The internal resistance of a battery is given by, $r = \dfrac{{\left( {V - E} \right)R}}{V}$ where $V$ is the voltage across the circuit, $E$ is the emf of the battery and $R$ is the resistance offered by the circuit.

Complete step by step answer:
Step 1: Sketch circuit diagram of the given arrangement.

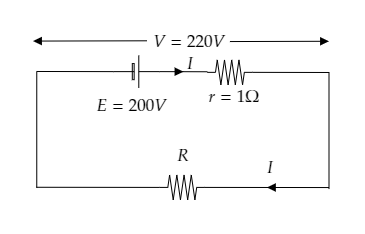
In the above figure, $I$ is the current in the circuit.
The emf of the storage battery is given to be $E = 200{\text{V}}$.
The emf of the dc main supply $V = 220{\text{V}}$ will be the potential difference across the circuit.
The internal resistance of the battery is given to be $r = 1\Omega$.
The potential drop across the internal resistance will be $Ir$.
The external resistance is $R$.
Step 2: Express the potential difference across the circuit to obtain the current in the circuit.
The potential difference across the circuit can be expressed as $V = E + Ir$ -------- (1)
Substituting for $E = 200{\text{V}}$, $V = 220{\text{V}}$ and $r = 1\Omega$ in equation (1) we get, $220 = 200 + \left( {I \times 1} \right) = 200 + I$
$\Rightarrow I = 220 - 200 = 20{\text{A}}$.
Thus the current in the circuit is $I = 20{\text{A}}$.
This same current flows through the internal resistance and the external resistance.
Step 3: Using Ohm’s law obtain the minimum value of $R$.
The potential difference across the external resistance is equal to the emf of the dc main supply $V = 220{\text{V}}$.
The current through external resistance is $I = 20{\text{A}}$.
Then Ohm’s law gives the external resistance as $R = \dfrac{V}{I}$ and on substituting the values we get, $R = \dfrac{{220}}{{20}} = 11\Omega$ .
Thus the minimum value of the external resistance is $R = 11\Omega$.

Hence the correct option is C.

Note:
Alternate method:
Given the internal resistance of the battery $r = 1\Omega$.
Also given the emf of the storage battery $E = 200{\text{V}}$ and emf of supply $V = 220{\text{V}}$.
Here $R$ is the external resistance connected across the storage battery.
Then the internal resistance of the battery is given by, $r = \dfrac{{\left( {V - E} \right)R}}{V}$ ------- (A)
Substituting for $r = 1\Omega$, $E = 200{\text{V}}$ and $V = 220{\text{V}}$ in equation (A) we get, $1 = \dfrac{{\left( {220 - 200} \right)R}}{{220}} = \dfrac{{20R}}{{220}}$
$\Rightarrow R = \dfrac{{220}}{{20}} = 11\Omega$

Thus we obtain the minimum value of the resistance as $R = 11\Omega$.