Question

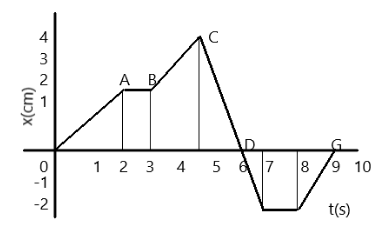
A dancer demonstrating dance steps along a straight line. The position time graph is given below. Find the average velocity of the dancer during time interval between $t = 4.5$ to $t = 9s$

(A) $1m/s$
(B) $- 1.33m/s$
(C) $2.75m/s$
(D) $- 0.89m/s$

Answer 1

Hint : For average velocity we only consider the start point and end point of the body, and do not consider the complete path taken by the body. It is also a vector quantity and thus we need to consider the direction of motion of the body.

Formula used: In this solution we will be using the following formula;
$\Rightarrow v = \dfrac{{{x_f} - {x_i}}}{{{t_f} - {t_i}}}$ where $v$ is the average velocity, ${x_f}$ is the final position, ${x_i}$ is the initial position, ${t_f}$ is the final time and ${t_i}$ is the initial time.

Complete step by step answer

In general, velocity can be defined as the time rate of change of displacement, and displacement is defined as the straight line joining the initial and final position in the direction of the final position. It is irrespective of the actual path taken.
Average velocity is simply given as the displacement of the positions considered divided by the overall time taken to traverse the position. It can be given mathematically as
$\Rightarrow v = \dfrac{{{x_f} - {x_i}}}{{{t_f} - {t_i}}}$ where ${x_f}$ is the final position, ${x_i}$ is the initial position, ${t_f}$ is the final time and ${t_i}$ is the initial time.
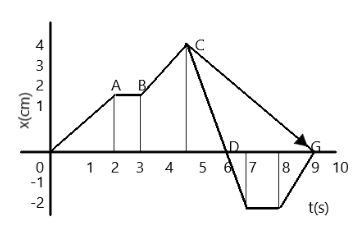
Hence, from the position-time graph, we see that ${t_i} = 4.5s$ , ${t_2} = 9s$ , ${x_i} = 4m$ , ${x_f} = 0m$ . This is the value corresponding to the arrow from C to G.
Thus inserting these values into the formula we have
$\Rightarrow v = \dfrac{{0 - 4}}{{9 - 4.5}}$ , hence by computation we have that
$\therefore v = \dfrac{{ - 4}}{{4.5}} = - 0.89m{s^{ - 1}}$
Thus, the correct answer is option D.

Note
We need to observe how all the position changes below the time axis is neglected. Usually, in application, displacement and velocity are used under situations where we can neglect the path taken but only the change in a particular direction is of interest. For example, in work done of a conservative force which is independent of the path taken. Hence, we use the displacement and not total distance covered.