Question

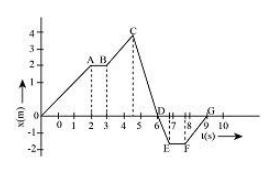
: A dancer demonstrating dance steps along a straight line. The position time graph (x-t) is as shown in the given figure. Find the average velocity for the dance steps depicted by AB.

(A) $1\;m{s^{ - 1}}$
(B) $1.33\;m{s^{ - 1}}$
(C) $2.75\;m{s^{ - 1}}$
(D) $0\;m{s^{ - 1}}$

Answer 1

To determine the value of the average velocity, we have to determine the magnitude of the dancer's displacement during AB's time interval. After getting the displacement's magnitude, we can obtain the correct average velocity value with the help time.

Complete step by step answer:
From the given graph, we can determine the position of the dancer at different times. So, with the help of different positions at different times, we can also determine the dancer's displacement.Here from the graph, we can see that the dancer's position at A is 2 m, and the dancer's position at B is also 2 m. So it means that the dancer covered zero distance from A to B and remains in its initial position. From this, we can understand that the dancer's initial and final position between AB is the same.
Now we will write the expression of displacement of the dancer.
$D = {x_2} - {x_1}$
Here, ${X_1}$ is the initial position of the dancer and ${X_2}$ is the final position of the dancer.
But we know that, The initial and final position of the dancer is the same, therefore we get${x_1} = {x_2} = x$.
Now we will substitute ${x_1} = {x_2} = x$ in the expression of displacement.
$\begin{array}{l} D = x - x\\\ D = 0\;m \end{array}$
From the graph, we can determine that the total time of AB is $t = 1\;s$.
Write the expression of the average velocity.
$v = \dfrac{D}{t}$
Now we will substitute the values of time and displacement in the above equation.
Therefore, we get
$\begin{array}{l} v = \dfrac{{0\;m}}{{1\;s}}\\\ v = 0\;m{s^{ - 1}} \end{array}$
Therefore, the average velocity for the dance steps depicted by AB is $0\;m{s^{ - 1}}$ and option (D) is correct.

Note: The average velocity gives information about how fast the displacement occurs in the given time. Here, displacement means the smallest distance between the dancer's original position and the final position. The displacement can be both positive as well as negative. But in the question, displacement is zero.