Question

A cylindrical vessel of height 500 mm has an orifice small hole at its bottom. The orifice is initially closed and water is filled in it up to height H. Now the top is completely sealed with a cap and the orifice at the bottom is opened. Some water comes out from the orifice and water level in the vessel becomes steady with the height of the water column being 200 mm. Find the fall in height in ml of water level due to the opening of the orifice. [Take atmospheric pressure $=1.0\times {{10}^{5}}N/{{m}^{2}},$ density of the water $=1000kg/{{m}^{3}}$ and $g=10m/{{s}^{2}}$ neglect any effect of surface tension]

Answer 1

Apply Bernoulli's principle at two cross-sections at the orifice and the top of the vessel. Take the height of the orifice as zero and the pressure at the orifice as atmospheric pressure and then apply Boyle's law and find out the value of height before the orifice is open.

Complete step by step answer:

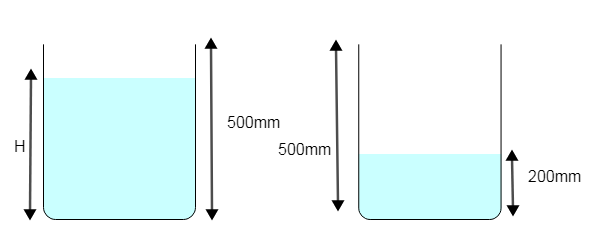
Let the pressure at the top of the vessel as P
Let the atmospheric pressure as $P_o$ and height after the water column becomes steady be h. we get applying Bernoulli's principle at top of the vessel and the orifice as
$P + \rho g h = P_o$
The Pressure at the top of the vessel in terms of atmospheric pressure
$P = P_o - \rho g h$
We know the values of density, g, h are given as g = 10 and h = 0.2 m and $\rho = 1000$ the value of the $P_o = 1 \times 10 ^5$
Substituting given values we get:
$P = 10^5 - (1000)(10)(0.2) = 98 \times 10^3$
Now we found the final value of pressure at the top of the container.
Let us apply Boyle’s law, we get
$P_i V_i = P_f V_f =$ Constant
Consider where the initial pressure at the top of the container is atmospheric pressure.
We get $10^5(A(0.5-H)) = 98\times 10^3 (A(0.5-0.2))$ where A is the cross-sectional area of a vessel
We get 0.5 - H = 0.294
H = 0.206 = 206 mm
So we found the initial height of the vessel as 206 mm
Hence the fall in height of water level is 206 - 200 = 6 mm
Using Boyle’s law Bernoulli principle we found the fall in height of the water level as 6mm

Note:
Here we need to understand that mention pressure at the top of the container is equal to the atmospheric pressure initially the lid was open.one of the possible mistakes that one can make in this kind of problem is that we may consider the initial pressure at the top of the container as zero and hence we need to take care of initial and final pressures.