Question

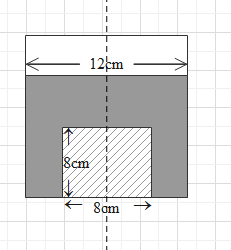
A cylindrical vessel of diameter 12cm contains 800$\pi c{{m}^{3}}$ of water. A cylindrical glass piece of diameter 8cm and height 8cm is placed in the vessel. If the bottom of the vessel under the glass piece is seen by the paraxial rays, locate its image. The index of refraction of glass is 1.5 and that of water is 1.33.

A. 9.2 cm above the bottom
B. 12.5 cm above the bottom
C. 7.1 cm above the bottom
D. 7.1 below the bottom

Answer 1

Hint: First, calculate the height of the water level when the glass piece is placed inside the container. Then use the formula to find apparent height i.e. $\dfrac{{{h}_{A}}}{{{h}_{R}}}=\dfrac{{{\mu }_{r}}}{{{\mu }_{i}}}$ at the two interfaces. First at the interface of glass and water and then at the interface of water and air.

Formula used:
$\dfrac{{{h}_{A}}}{{{h}_{R}}}=\dfrac{{{\mu }_{r}}}{{{\mu }_{i}}}$

Complete step by step answer:
It is given that the volume of water in the container is 800$\pi c{{m}^{3}}$. Initially, the water level will be at some height from the bottom of the container. Then when the cylindrical glass piece is placed in the vessel, the level of the water will increase because the glass piece will occupy some volume inside the container. Let the new height of water level be h. Let us calculate the value of h.
The diameter of the cylindrical glass piece is given to be 8cm. This means that the radius (r) of the cylinder is 4cm. The height (h’) of this cylinder is 8cm.
Hence, the volume of the cylindrical glass piece is ${{V}_{g}}=\pi {{r}^{2}}h'=\pi ({{4}^{2}})(8)=128\pi c{{m}^{3}}$.
The total volume occupied by water and the glass piece is equal to ${{V}_{w}}+{{V}_{g}}=800\pi +128\pi =928\pi c{{m}^{3}}$ .
This total volume is in the form of a cylinder of radius 6cm anf height h.
Hence, $928\pi =\pi {{(6)}^{2}}.(h)$
$\Rightarrow 928=36h$
$\Rightarrow h=\dfrac{928}{36}=25.77cm$.
The rays from the bottom of the container will refract twice. First, at the interface of the glass and water. Then, at the interface of water and air. Hence, there will be two images formed. The person will see the final image.
When light rays from the bottom refract at the interface of glass and water, the bottom will appear to be raised. The original height (${{h}_{R}}$) of the bottom point from the interface is called real height and the new height from the same interface at which the point appears is called apparent height (${{h}_{A}}$).
The relation between ${{h}_{R}}$ and ${{h}_{A}}$ is given as $\dfrac{{{h}_{A}}}{{{h}_{R}}}=\dfrac{{{\mu }_{r}}}{{{\mu }_{i}}}$.
Here, ${{\mu }_{r}}$ and ${{\mu }_{i}}$ are the refractive indices of the mediums where the rays are refracted and incident respectively.
In this case, ${{h}_{R}}=8cm$, ${{\mu }_{r}}=1.33$ and ${{\mu }_{i}}=1.5$.
Hence, $\dfrac{{{h}_{A}}}{8}=\dfrac{1.33}{1.5}$
$\Rightarrow {{h}_{A}}=8\times \dfrac{1.33}{1.5}=7.09cm$.
Therefore, the first image is formed at a distance of 7.09cm from the interface of glass and water. This means it is at a distance of 0.91cm above the bottom.
This image will act as an object for the interface of water and air. Hence, the bottom will appear to be raised more.
In this case, the real height is equal to height of water minus height of the first image from the bottom. i.e. $25.77-0.91=24.86cm$
Therefore, ${{h}_{R}}=24.86cm$, ${{\mu }_{r}}=1$ and ${{\mu }_{i}}=1.33$.
Hence, we get,
$\dfrac{{{h}_{A}}}{24.86}=\dfrac{1}{1.33}$
$\Rightarrow {{h}_{A}}=24.86\times \dfrac{1}{1.33}=18.69cm$
Therefore, the final image of the bottom will be formed at a distance of 18.69cm from the surface of water. This means that from the bottom surface, the image will form at a distance of $25.77-18.69=7.08\approx 7.1cm$.
Therefore, the image of the bottom point is 7.1 cm above the bottom surface.
Hence, the correct option is C.

Note: We can also use the formula for lateral shift of a point when the rays of light pass from different mediums. The lateral shift is given by $t\left( 1-\dfrac{1}{\mu } \right)$, where t is the thickness of the medium through which the rays are passing and $\mu$ is the refractive index of that medium. Here, there will be two lateral shifts and the total shift will be the sum of the both.