Question

A cylindrical vessel filled with water up to height h stands on a horizontal plane. The side wall of the vessel has a plugged circular hole touching the bottom. The coefficient of friction between the bottom of the vessel and plane is $\mu$ and the total mass of the water vessel is m. What should be minimum diameter of hole so that the vessel begins to move on the floor if plug is removed (here density of water is $\rho$):
$\begin{aligned} & \text{A}\text{. }\sqrt{\dfrac{2\mu m}{\pi \rho h}} \\\ & \text{B}\text{. }\sqrt{\dfrac{\mu m}{2\pi \rho h}} \\\ & \text{C}\text{. }\sqrt{\dfrac{\mu m}{\rho h}} \\\ & \text{D}\text{. none} \\\ \end{aligned}$

Answer 1

The cylindrical vessel is filled with water at some height. Once the plugged is removed, water will start flowing out of the cylinder with a particular velocity. We will apply Torricelli’s theorem to calculate the velocity of the emerging water and balancing the impulsive force with the static frictional force will give the required diameter of the hole.

Formula used:
Velocity of water coming out of a hole:
$v=\sqrt{2gh}$
Frictional force: $\mu mg$

Complete step by step answer:
When the plug is removed, water will start coming out of the hole. As we know, Torricelli’s theorem is applied for a liquid column in a container leaking out of a hole, and the theorem gives us the momentary velocity of fluid just outside of the hole.
We are given that a cylindrical vessel filled with water up to height h stands on a horizontal plane, and the sidewall of the vessel has a plugged circular hole touching the bottom.

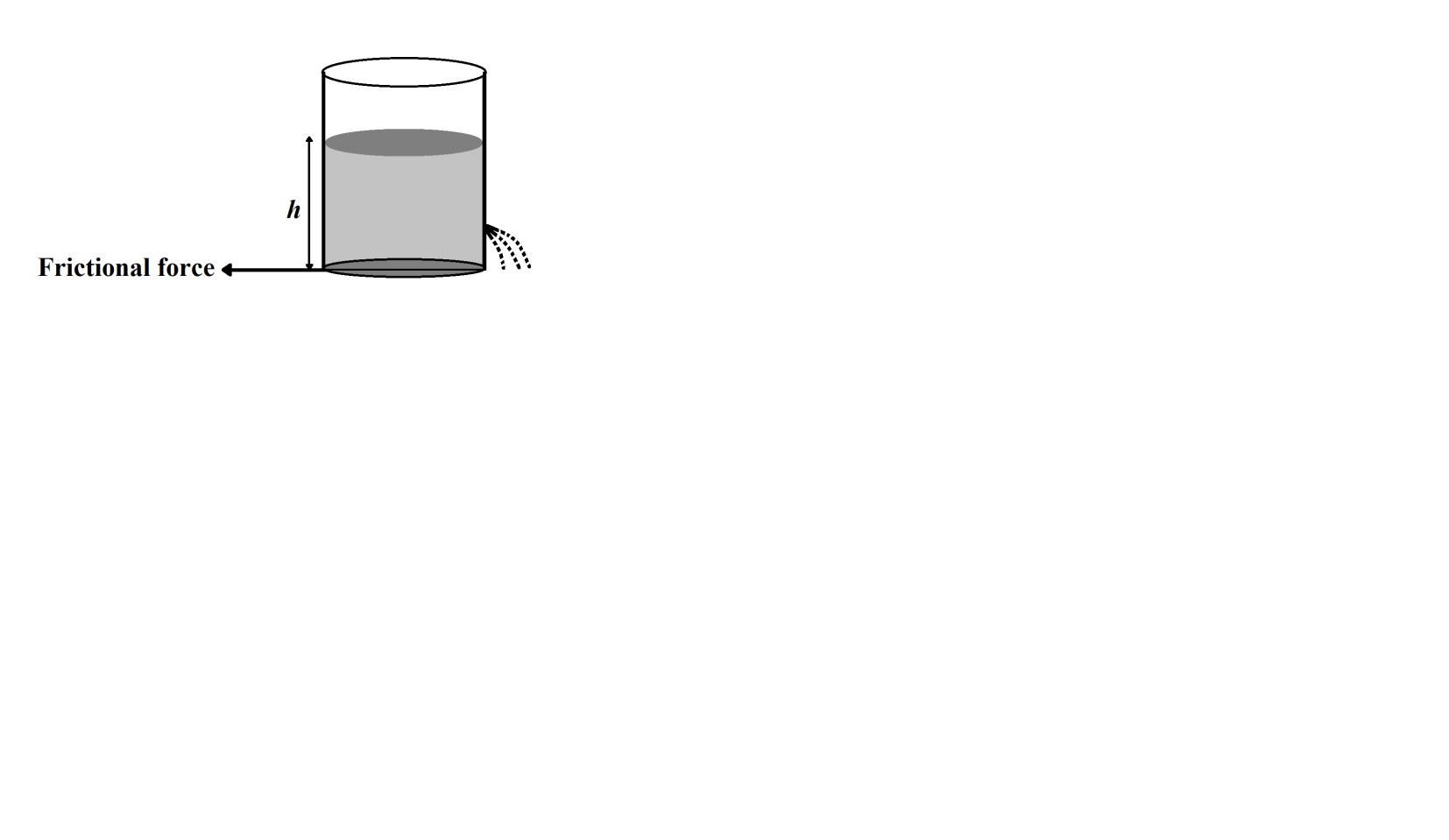
By applying Torricelli’s theorem,
$v=\sqrt{2gh}$
Where $v$ the velocity of water coming out of a hole is, $g$ is the gravitational acceleration and $h$ is the height of the water column above the hole.
As the water flows out of the hole, it will apply an impulsive force on to the container.
Now, the impulse of a force $F$ acting for a time $\Delta t$ is equal to $F\Delta t$ or $\Delta \left( mv \right)$
Now, as the velocity of water coming out of the hole is constant at the moment when water column height is $h$,
So, $\Delta \left( mv \right)=v\Delta \left( m \right)$
As we know, the mass of a fluid is the product of its volume and density.
So,
Mass of water column will be,
$M=\rho V$
Where, $\rho$ is the density of water and $V$ is the volume of water in the container above hole.
Now, as we know, the volume of a cylinder is equal to the product of base area and height,
So, the volume of the water column is,
$V=Ah$
Where,
$A$ is the base area and $h$ is the height of the water column.
Now, as the base is circular, let the diameter is $d$
So, $A=\dfrac{\pi {{d}^{2}}}{4}$
Thus, $V=Ah=\dfrac{\pi {{d}^{2}}h}{4}$
And, $m=\rho V=\dfrac{\pi \rho {{d}^{2}}h}{4}$
And, the Impulsive force,
$\Delta \left( mv \right)=v\Delta \left( m \right)=v\Delta \left( \dfrac{\pi \rho {{d}^{2}}h}{4} \right)$
As, $\pi ,\rho ,d$ are constant,
So, the Impulsive force,
$v\Delta \left( \dfrac{\pi \rho {{d}^{2}}h}{4} \right)=\dfrac{\pi \rho {{d}^{2}}v}{4}\Delta \left( h \right)$
We get,
$F\Delta t=\dfrac{\pi \rho {{d}^{2}}v}{4}\Delta \left( h \right)$
$F=\dfrac{\pi \rho {{d}^{2}}v}{4}\times \dfrac{\Delta \left( h \right)}{\Delta t}$
Now, $\dfrac{\Delta \left( h \right)}{\Delta t}$ is the rate of decline of the height of the water column, which will be equal to the velocity of the water.
$F=\dfrac{\pi \rho {{d}^{2}}{{v}^{2}}}{4}$
So, we have the impulsive force, $\dfrac{\pi \rho {{d}^{2}}{{v}^{2}}}{4}$
Now, at the container and surface contact, friction will act on the container opposite the applied force, i.e. impulsive force.
Force of friction is: $\mu R$ where $R$ is the normal reaction at the contact and $\mu$ is the coefficient of friction at the surface of contact.
Now, the container is resting on the floor, so its weight will balance the normal reaction.
So, $R=mg$
Where,
$m$ is the total mass of the container.
Thus, the frictional force is $\mu mg$
So, in order to make the container move, the impulsive force must be greater than the static frictional force on the container.
Thus, $\dfrac{\pi \rho {{d}^{2}}{{v}^{2}}}{4}>\mu mg$
That means,
${{d}^{2}}>\dfrac{4\mu mg}{\pi \rho {{v}^{2}}}$
Substituting, $v=\sqrt{2gh}$
We get,
$\begin{aligned} & {{d}^{2}}>\dfrac{4\mu mg}{\pi \rho {{\left( \sqrt{2gh} \right)}^{2}}} \\\ & {{d}^{2}}>\dfrac{2\mu mg}{\pi \rho gh} \\\ & {{d}^{2}}>\dfrac{2\mu mg}{\pi \rho gh} \\\ \end{aligned}$
The minimum value of diameter would be $\sqrt{\dfrac{2\mu m}{\pi \rho h}}$
Hence, the correct option is A.

Note:
Students should note that at a particular height of the column of water, the emerging water will have a fixed value of velocity. As the height of column changes, velocity of emerging water changes as well. For a container to move due to flowing water, impulsive force must be greater than the static frictional force.