Question

A cylindrical tube open at both ends has a fundamental frequency $n$ in air. The tube is dipped vertically in water so that half of it is immersed in water. The fundamental frequency of air column is:
A. $\dfrac{n}{2}$
B. $n$
C. $2n$
D. $4n$

Answer 1

The fundamental frequency is defined as the lowest frequency that is obtained by the oscillations of the object. Here, the tube is immersed in water, so, we will calculate the fundamental frequency in the case of a closed tube.

Formula used:
The formula used to calculate the fundamental frequency of the air column is given by
$n' = \dfrac{v}{{4L}}$
Here, $n$ is the fundamental frequency, $v$ is the velocity of the frequency, and $L$ is the length of the tube. We are using the fundamental frequency in the case of a closed tube because the tube is immersed in water.

Complete step by step answer:
Consider a cylindrical tube that is open at both ends and is immersed in the water. The length of the cylindrical tube is $L$ . Let half of the tube be immersed in water.

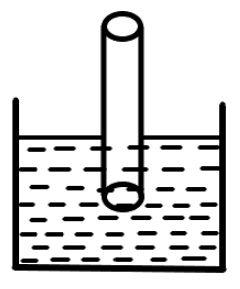
Now, as the tube is open, therefore, open fundamental frequency, $n = \dfrac{v}{{2L}}$
Now, half of the tube is immersed in the water, therefore, the length of the tube in the water will become half. Therefore, the length of the tube in water $= \dfrac{L}{2}$.

Now, when half of the tube is immersed in water, then the tube will behave as a closed tube. Therefore, let the fundamental frequency of the closed pipe is $n'$ and is given by,
$n' = \dfrac{v}{{4L}}$
Now, the length of the tube in the water is half. Therefore, the above equation becomes
$n' = \dfrac{v}{{4 \times \dfrac{L}{2}}}$
$\Rightarrow \,n' = \dfrac{v}{{2L}}$
$\therefore \,n' = n$
Hence, the fundamental frequency of the air column is $n$ .

Hence, option B is the correct option.

Note: In simple terms we can also provide the solution as: When the tube is immersed in water, the medium of the propagation of oscillations will change. As a result, the speed and wavelength of the wave will also change keeping the frequency constant. Therefore, we get the fundamental frequency of the air column is $n$ when the tube is immersed in water.