Question

A cylindrical tube, open at both ends, has a fundamental frequency ν in air. The tube is dipped vertically in water so that half of it is in water. The fundamental frequency of the air column now is (this question has multiple correct options).
A. $\dfrac{\nu }{2}$
B. $\nu$
C. $\dfrac{3\nu }{4}$
D. $2\nu$

Answer 1

Approach the question by considering two cases. One, when the tube is in air other when the tube is half dipped in water. Recall that the lowest possible natural frequency is called the fundamental frequency and hence find the wavelength present in a tube of length L and then substitute in the expression of frequency. Keeping V (speed of sound in air) constant, repeat the above step for the second case and hence see the relation between the frequencies in both cases.
Formula used:
Expression for frequency,
$f=\dfrac{V}{\lambda }$

Complete answer:
In the question we are given a cylindrical tube that is open at the both ends. It is said to have a fundamental frequency of ν in air. Now we are dipping this tube vertically in water such that half of the tube gets filled with water and we are asked to find the fundamental frequency of the air column now.
We can approach this question by considering two cases: one when the tube is in air and the other when the tube is half dipped in water.
Case 1:

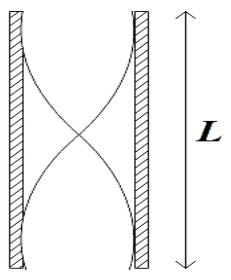
Here the tube is open at both ends.
We know that the distance between two adjacent nodes or the distance between two adjacent antinodes is$\dfrac{\lambda }{2}$. Here in the figure we have two adjacent antinodes and the distance between them is equal to the length of the tube. Therefore,
$\Rightarrow \dfrac{\lambda }{2}=L$
$\Rightarrow \lambda =2L$ ………………….. (1)
The fundamental frequency f is given by,
$f=\dfrac{V}{\lambda }$ …………………. (2)
Where, V is the speed of sound in air and λ is the wavelength.
In the question we are given that the fundamental frequency as ν and also substituting (1) in (2), we get the fundamental frequency in this case as,
$\nu =\dfrac{V}{2L}$ ………………………. (3)
Case 2:

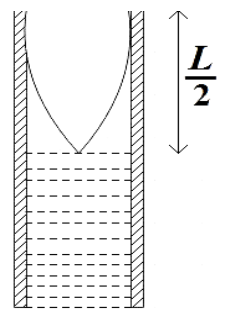
Now we are dipping half of the tube in water and it acts like a tube that is closed at one end.
We know that distance between adjacent node and an antinode is $\dfrac{\lambda }{4}$ and this is equal to half the length of the pipe,
$\Rightarrow \dfrac{\lambda '}{4}=\dfrac{L}{2}$
$\Rightarrow \lambda '=\dfrac{4L}{2}$
Fundamental frequency will be,
$\Rightarrow f'=\dfrac{V}{\lambda '}=\dfrac{V}{\dfrac{4L}{2}}$
$\Rightarrow f'=\dfrac{V}{2L}$ …………………………. (4)
From (3) and (4), we see that fundamental frequency in air ν and fundamental frequency after half dipping the tube in water is the same.
Therefore, the fundamental frequency of the air column after dipping half of the tube in water is ν.

Hence, the answer to the question is option B.

Note:
Since the fundamental frequency is the least possible natural frequency, in the expression for the wavelength given by,
$\lambda =\dfrac{2L}{n}$
We could substitute n=1 as the case is on fundamental frequency and hence,
$L=\dfrac{\lambda }{2}$
This is clearly represented in the figure.
We have standard expressions for fundamental frequencies in open tube and in tube closed at one end, given respectively as,
$\nu =\dfrac{V}{2L}$
$\nu '=\dfrac{V}{4L}$
So, as an alternative method, you could simply substitute for L in this relation to find the answer to the question.