Question

A cylindrical tank of diameter 35 cm is full of water. If 11 litres of water is drawn out, the water level in the tank will drop by________.
(a) $10\dfrac{1}{2}\text{ cm}$
(b) $11\dfrac{3}{7}\text{ cm}$
(c) $12\dfrac{6}{7}\text{ cm}$
(d) 14 cm

Answer 1

Hint: Assume that initially the height of the water level in the cylindrical tank is ‘h’. When 11 litres of water is drawn then assume that the height of water level in the cylindrical tank becomes ‘k’. We have to find the value of ‘h – k’ in cm. Use the volume relation given by: volume of water in the cylindrical initially = volume of water left in the tank + volume of water drawn (11 litres). Apply the formula for volume of cylinder $=\pi {{r}^{2}}h$, where ‘r’ is the radius of the cylinder and ‘h’ is the height of the cylinder. To convert litres into cubic centimeters, use the relation: $1\text{ litres}=1000\text{ c}{{\text{m}}^{3}}$.

Complete step-by-step answer:
We have been provided with a cylindrical tank with diameter 35 cm. Therefore,
$\text{radius}=r=\dfrac{\text{diameter}}{2}=\dfrac{35}{2}\text{ cm}$

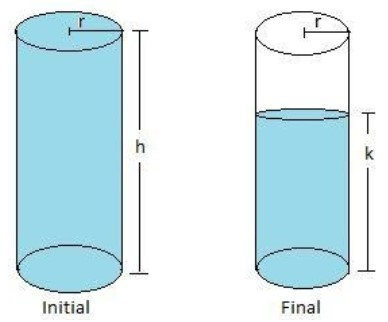
Now, let us assume that, initially the height of the water level in the cylindrical tank is ‘h’. It is given that 11 litres of water is drawn from the tank. Therefore, assume that, finally, the level of water in the tank becomes ‘k’. We have to determine the decrease in water level, that is ‘h – k’.
First let us convert 11 litres into cubic cm, so that we can get the height in centimeters.
We know that: $1\text{ litres}=1000\text{ c}{{\text{m}}^{3}}$. Therefore, $11\text{ litres}=11000\text{ c}{{\text{m}}^{3}}$.
Now, applying the volume relation: volume of water in the cylindrical initially = volume of water left in the tank + volume of water drawn (11 litres). We get,
$\begin{aligned} & \pi {{r}^{2}}h=\pi {{r}^{2}}k+11000 \\\ & \Rightarrow \pi {{r}^{2}}h-\pi {{r}^{2}}k=11000 \\\ & \Rightarrow \pi {{r}^{2}}(h-k)=11000 \\\ & \Rightarrow (h-k)=\dfrac{11000}{\pi {{r}^{2}}} \\\ \end{aligned}$
Substituting the values: $\pi =\dfrac{22}{7}$ and $r=\dfrac{35}{2}$, we get,
$\begin{aligned} & (h-k)=\dfrac{11000}{\dfrac{22}{7}\times {{\left( \dfrac{35}{2} \right)}^{2}}} \\\ & \Rightarrow (h-k)=\dfrac{11000}{\dfrac{22}{7}\times \dfrac{35}{2}\times \dfrac{35}{2}} \\\ & \Rightarrow (h-k)=\dfrac{11000\times 7\times 2\times 2}{22\times 35\times 35} \\\ \end{aligned}$
Cancelling the common factors, we get,
$(h-k)=\dfrac{80}{7}\text{ cm}$
Converting this improper fraction into mixed fraction, we get,
$(h-k)=11\dfrac{3}{7}\text{ cm}$
Hence, option (b) is the correct answer.

Note: We have used the value of $\pi =\dfrac{22}{7}$ because nothing has been provided to us and using this value will make our calculation easy. Also, we have converted the volume, given in litres, into cubic centimeters because we have to find the level of water in $cm^3$ and without using the required conversion we will get a wrong answer.Using the volume relation given by: volume of water in the cylindrical initially = volume of water left in the tank + volume of water drawn (11 litres) is the key point for solving this question.