Question

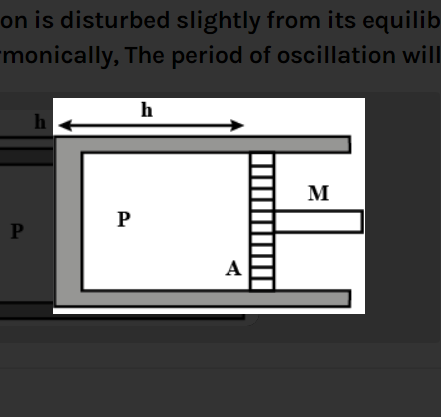
A cylindrical piston of mass M slides smoothly inside a long cylinder closed at one end, enclosing a certain mass of a gas. The cylinder is kept with its axis horizontal. If the piston is slightly compressed isothermally from its equilibrium position, it oscillates simple harmonically, the period of oscillation will be

a)$T=2\pi \sqrt{\dfrac{Mh}{PA}}$
b) $T=2\pi \left( \dfrac{MA}{Ph} \right)$
c) $T=2\pi \left( \dfrac{M}{PAh} \right)$
d) $T=2\pi \left( MPhA \right)$

Answer 1

Let the piston be displaced through distance x towards left then volume decrease and pressure increase. Since no heat is being added into the system of piston and cylinder, we can assume it to be an isothermal process. By using the equation for the isothermal process:$PV=C$ , we can find out the increase in pressure inside the cylinder. The excess pressure developed inside the cylinder will act as a restoring force. Then by using the formula: $F=-kx$ and $F=\Delta PA$, find the value of spring constant k. Also, we know that: $\omega =\sqrt{\dfrac{k}{m}}$ and $T=\dfrac{2\pi }{\omega }$, find the value of time period T.

Formula used:
$F=-kx$, where F is force acting on spring, k is the spring constant and x is the displacement
$F=\Delta PA$, where F is force acting on spring, $\Delta P$ is the change in pressure and A is the cross-section area of the piston
$\omega =\sqrt{\dfrac{k}{m}}$, where $\omega$ is the angular velocity, k is the spring constant and m is the mass
$T=\dfrac{2\pi }{\omega }$ , where T is the time period and $\omega$ is the angular velocity

Complete step by step answer:
We have: $PV=C$
By differentiation the above equation, we gat:
$dP\times V+PdV=0$
Since,
$\begin{aligned} & V=Ah \\\ & dV=Ax \\\ \end{aligned}$
So, we have:
$\begin{aligned} & \Rightarrow dP\left( Ah \right)=-P\left( Ax \right) \\\ & \Rightarrow dP=-\dfrac{Px}{h} \\\ & \therefore \Delta P=-\dfrac{Px}{h} \\\ \end{aligned}$
As we know that, this excess pressure is responsible for providing the resting force F to the piston of mass of M.
So, we can write:
$\begin{aligned} & F=\Delta P\times A \\\ & =-\dfrac{PAx}{h}......(1) \end{aligned}$
Also, $F=-kx......(2)$
By comparing equation (1) and equation (2), we get:
$k=\dfrac{PA}{h}$
Now, as we know that: $\omega =\sqrt{\dfrac{k}{m}}$
So, we get:
$\omega =\sqrt{\dfrac{PA}{Mh}}$
Also, $T=\dfrac{2\pi }{\omega }$
Therefore, time period is: $T=2\pi \sqrt{\dfrac{Mh}{PA}}$

So, the correct answer is “Option A”.

Note:
In this question the time period(frequency) of the simple harmonic motion needs to be calculated. Simple harmonic motion is a special type of periodic motion where the restoring force on the moving object is directly proportional to the object's displacement magnitude and acts towards the object's equilibrium position. In simpler words the object after being disturbed from its mean position keeps coming back to its mean position until equilibrium is established. Mass on a spring is a general example of Simple Harmonic Motion.