Question
Question: A cylindrical glass tube is partially filled with water to create an air column of length \(0.1m\). ...
A cylindrical glass tube is partially filled with water to create an air column of length 0.1m. The air column is in resonance, in its fundamental mode, with a tuning fork. The level of the water is now lowered and the next resonance is observed at 0.35m. The end correction is?
A.0.025m
B.0.020m
C.0.015m
D.0.010m
Solution
The partially filled glass tube signifies that it is closed at one end and open at the other. A node is formed at the closed end but an antinode is formed at the open end. We shall find the end correction by finding the velocity of wave in each case and then both the equations as we are given the length of tube in its fundamental mode and at a harmonic.
Complete answer:
The fundamental wavelength is the wavelength at which the wave exhibits resonance for the first time. the subsequent wavelengths at which the wave shows resonance are called harmonics.
The wave velocity, v is given as:
v=λν
Where,
λ= wavelength
ν= frequency of wave
In first case, length of air column =l1+e
This length is equal to one-fourth of the wavelength in the fundamental mode.
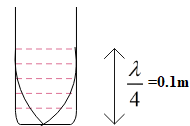
⇒4λ=l1+e
⇒λ=4(l1+e)
Therefore, velocity of wave is given as: v=4(l1+e)ν …………. Equation (1)
In the second case, length of air column =l2+e
This length is equal to three-fourth of the wavelength in the first harmonic mode.
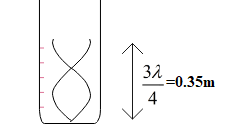
⇒43λ=l2+e
⇒λ=34(l2+e)
Therefore, velocity of wave is given as: v=34(l2+e)ν …………. Equation (2)
Since the wave velocity remains constant, thus equating equations (1) and (2),
⇒4(l1+e)ν=34(l2+e)ν
Cancelling 4 and νfrom both sides, we get
⇒(l1+e)=3(l2+e)⇒3l1+3e=l2+e⇒2e=l2−3l1
Now we have l1=0.1m and l2=0.35m,
⇒2e=0.35−3(0.1)⇒2e=0.35−0.30⇒2e=0.05⇒e=20.05
∴e=0.025m
Note:
If we create a wave in a medium that has no boundaries, this wave never meets the boundary and there is nothing stopping the wave from making a wave of any wavelength or frequency. However, if we confine this wave into a medium that has boundaries, this wave will reflect when it meets the boundary. Thus, standing waves are formed. Standing waves are formed of only selected preferred wavelengths and frequencies.
