Question

A cylindrical bucket, 32cm high with a radius of base 18cm, is filled with sand. This bucket is emptied on the ground and a conical heap of sand is formed. If the height of the conical heap is 24cm, then find the radius and slant height of the heap.

Answer 1

Hint: First find the volume of the cylinder by given data using formula $\pi {{r}^{2}}h$ where r and h is the radius and height of the cylinder. Then equate the value with the volume of cone formula which is $\left( \dfrac{\pi {{r}^{2}}h}{3} \right)$ where r and h is radius and height of cone and find the value of radius then find the value of slant height using formula $\sqrt{{{r}^{2}}+{{h}^{2}}}$ .

“Complete step-by-step answer:”
As the sand was contained in a cylindrical bucket, we can say that the amount of sand in the bucket is obtained by finding the volume of the cylindrical bucket.

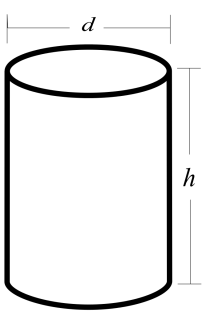
For finding the volume of a cylindrical bucket we will use the formula $\pi {{r}^{2}}h$ where r represents the radius of the base of the bucket, h represents the height and $\pi$ has value 3.14.
So the volume of the bucket is,
$V=\pi {{r}^{2}}h$
Substituting the given values, we get
$V=\pi \times {{\left( 18 \right)}^{2}}\times 32$
This is the volume of the cylinder.
Now as we know that the sand was drained out of the cylinder to make a conical heap of height 24cm.
So, the volume of the cone is same as the volume of the cylinder, i.e.,
${{V}_{cone}}=\pi \times {{\left( 18 \right)}^{2}}\times 32...........(i)$.

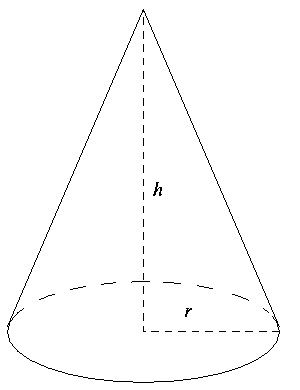
Now we are given the height of the cone, we can get the radius of base by using the volume of the cone formula, that is, $\dfrac{\pi {{r}^{2}}h}{3}$ , where h is height of cone and r is radius of base.
So we can represent it as,
$\dfrac{\pi {{r}^{2}}h}{3}=\pi \times {{\left( 18 \right)}^{2}}\times 32$
Cancelling $\pi$ from both the sides, and simplifying, we get
$\dfrac{{{r}^{2}}h}{3}={{\left( 18 \right)}^{2}}\times 32$
Now the height of the cone is given as 24cm, substituting this in above equation, we get
$\begin{aligned} & \dfrac{{{r}^{2}}(24)}{3}={{\left( 18 \right)}^{2}}\times 32 \\\ & \Rightarrow {{r}^{2}}(8)={{\left( 18 \right)}^{2}}\times 32 \\\ & \Rightarrow {{r}^{2}}=\dfrac{{{\left( 18 \right)}^{2}}\times 32}{8} \\\ & \Rightarrow {{r}^{2}}={{\left( 18 \right)}^{2}}\times 4 \\\ & \Rightarrow {{r}^{2}}={{\left( 18 \right)}^{2}}\times {{2}^{2}} \\\ \end{aligned}$
Taking square root on both sides, we get
$r=18\times 2=36$
Now we have to find the slant height of the cone, its formula is given as $\sqrt{{{r}^{2}}+{{h}^{2}}}$ where r is radius of base and h is height of cone.
$l=\sqrt{{{r}^{2}}+{{h}^{2}}}$
Now by substituting values ‘r=36cm’ and ‘h = 24cm’ we get,
$\begin{aligned} & l=\sqrt{{{36}^{2}}+{{24}^{2}}} \\\ & \Rightarrow l=\sqrt{1296+576} \\\ & \Rightarrow l=\sqrt{1872} \\\ \end{aligned}$
Which is further simplified as,
$\begin{aligned} & l=\sqrt{{{12}^{2}}\times 13} \\\ & \Rightarrow l=12\sqrt{13} \\\ \end{aligned}$
Hence, the slant height of the cone is equal to $12\sqrt{13}cm$
Therefore, the radius and slant height of cone is 36cm and $12\sqrt{13}cm$ respectively.

Note: Students confused how slant height can be represented as $\sqrt{{{r}^{2}}+{{h}^{2}}}$ , where r is the radius and h is the height.This can be obtained from pythagoras theorem.Students should not be confused with slant height and height of the cone as they both are different which is shown in above figure.
Another approach is instead of keeping the values as it is, $V=\pi \times {{\left( 18 \right)}^{2}}\times 32$
We can solve this and then substitute in the volume of the cone. But this becomes very tedious and lengthy to solve the value of the volume of the cylinder.