Question

A cylindrical block made of wood $\left( density=650kg{{m}^{-3}} \right)$ of base area $30c{{m}^{2}}$ and height $54cm$, floats in a liquid of density $900kg{{m}^{-3}}$. The block will be depressed slightly and then it is released. What will be the time period of the oscillations of the block which will be similar to that of a simple pendulum of length?
$\begin{aligned} & A.52cm \\\ & B.26cm \\\ & C.39cm \\\ & D.65cm \\\ \end{aligned}$

Answer 1

Find out the equation for the extra buoyant force occurring when the block is slightly displaced for a small distance from equilibrium. This extra buoyant force will be equivalent to the product of the mass and the acceleration. This will help you in answering this question.

Complete step by step answer:
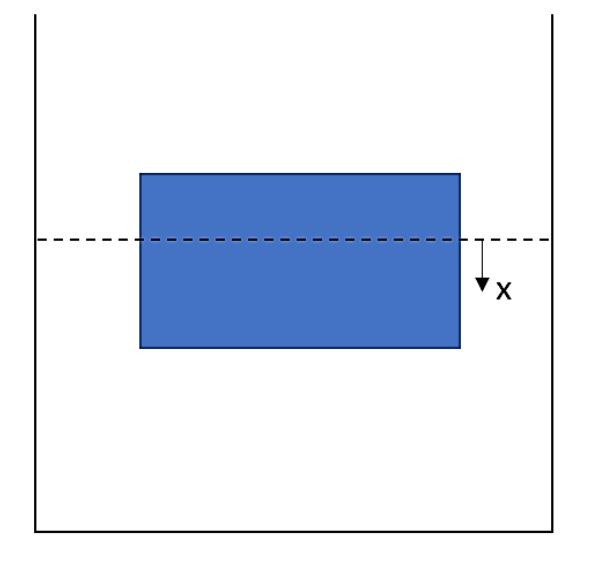
let us assume that the block is displaced further by a small distance from the equilibrium. Therefore extra buoyant force will be equivalent to the product of the mass and the acceleration.
$\text{extra bouyant force = mass}\times \text{acceleration}$
The extra buoyant force can be expressed in the form of equation as,
$-{{\rho }_{L}}Axg={{\rho }_{b}}Ah\dfrac{{{d}^{2}}x}{d{{t}^{2}}}$
It has been given in the question that the density of the liquid is,
${{\rho }_{L}}=900kg{{m}^{-3}}$
The density of the wooden block will be,
${{\rho }_{b}}=650kg{{m}^{-3}}$
The base area is mentioned as,
$A=30c{{m}^{2}}$
Height of the block will be,
$h=54cm$
Substituting this in the equation will give,
$-900\times 30\times {{10}^{-4}}xg=650\times 30\times {{10}^{-4}}\times 54\times {{10}^{-2}}\dfrac{{{d}^{2}}x}{d{{t}^{2}}}$
Simplifying this equation will give,
$\dfrac{{{d}^{2}}x}{d{{t}^{2}}}=\left( \dfrac{-g}{39 \times {10}^{-2}} \right)x$
That is we can write that,
${{\omega }^{2}}=\left( \dfrac{g}{39 \times {10}^{-2}} \right)$
Where $\omega$ be the angular velocity.
For a simple pendulum, the angular velocity is given by the equation,
${{\omega }^{2}}=\left( \dfrac{g}{L} \right)$
When we compare this two relation, we can get to know that the length of the rod will be calculated as,
$L=39cm$

So, the correct answer is “Option C”.

Note: Buoyant force which is otherwise known as buoyant force is defined as an upward force or thrust exerted by a fluid that prevents the weight of a partly or completely immersed body. The pressure increases with depth because of the weight of the overlying fluid in a column of fluid.