Question
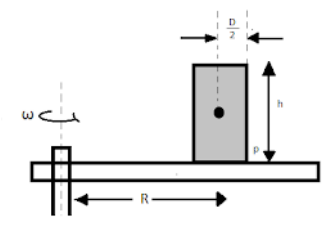
Question: A cylinder rests on a horizontal rotating disc, as shown in the figure. Find at what angular velocit...
A cylinder rests on a horizontal rotating disc, as shown in the figure. Find at what angular velocity, ω the cylinder falls of the disc, if the distance between the axes of the disc and cylinder is R , and the coefficient of friction μ>hd , where D is the diameter of the cylinder and h is its height.
\left( A \right)\sqrt {\dfrac{{3Dg}}{{hR}}} \\\
\left( B \right)\sqrt {\dfrac{{3Dg}}{{2hR}}} \\\
\left( C \right)\sqrt {\dfrac{{Dg}}{{hR}}} \\\
\left( D \right)None{\text{ }}of{\text{ }}these \\\
Solution
Hint : In order to solve this question, we are going to first see the condition of equilibrium where the torque about the centre of mass becomes zero. The angular velocity of the cylinder is calculated by using the limiting condition for the coefficient of equilibrium as given in question.
If f is the force of friction, and N is the normal force.
Thus, f=μN
Complete Step By Step Answer:
In the state of equilibrium, the two opposite forces balance each other and are equal, thereby making the torque about the centre of mass equal to zero,
In mathematical form,
f×2h=N×2d
Where f is the force of friction, and N is the normal force.
Thus, f=μN
Putting this in the above equation, we get
\mu N \times \dfrac{h}{2} = N \times \dfrac{d}{2} \\\
\Rightarrow \mu = \dfrac{d}{h} \\\
As it is given in the question that μ>hd is the limiting condition for it.
The force that acts on the block will be
f=μN=hNd
Now, if we balance the forces in the horizontal direction,
mω2R=μN=hNd
Here, N is the normal force, thus, it is equal to mg .
Putting this in the above equation and finding the value of ω .
ω=hRDg
Hence, option (C)hRDg is the correct answer.
Note :
In order to stay steady and avoid toppling, the cylinder must lie on a surface with a coefficient of friction greater than hd . That is why we are given the limiting value of the coefficient of friction in question only. Do not forget to take this condition in consideration. Torque about the centre of mass is always zero.
