Question

A cylinder of weight $W$ and radius$R$ is to be raised onto a horizontal step of height $h$ as shown in the figure. A rope is wrapped around the cylinder and pulled horizontally with force $F$ . Assuming the cylinder does not slip on the step; find the minimum force $F$ necessary to raise the cylinder.

Answer 1

It is asked in the problem to find the minimum force needed to raise the cylinder. This force can be found out by balancing torques acting on opposite two sides if the cylinder. One of the torques is produced by the force needed to raise the cylinder and the other is the gravitational force acting on the cylinder due to its weight.

Formula used:
The torque produced by force $F$ is: ${\tau _1} = F\left( {2R - h} \right)$
The torque produced by the weight of cylinder is: ${\tau _2} = W\sqrt {2Rh - {h^2}}$

Complete step by step answer:
The cylinder is given with radius $R$ and does not slip on the step. The force acting to raise the cylinder from the step is in horizontal direction. This force acts in the direction of motion. In order to calculate the minimum force, one needs to balance all the torques. The force given by $F$ is the minimum force needed to raise the cylinder on the step of height$h$ .
When the cylinder is just about to lift up, the perpendicular component of force produces a torque. The distance from step of height $h$ to the other end of the cylinder is given by $2R - h$ . Thus, the torque here becomes,
${\tau _1} = F\left( {2R - h} \right)$ $\to (1)$

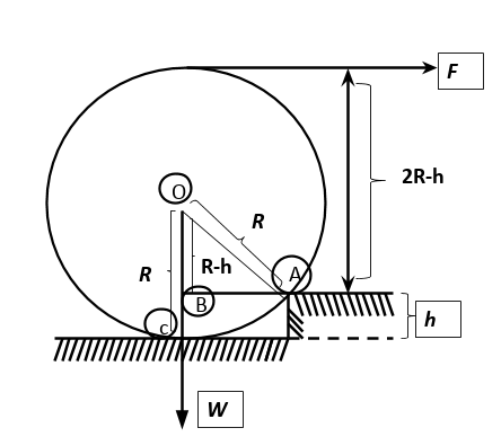
The component of the weight of the cylinder given by $W$ is acting downwards with respect to the cylinder. Then, the torque produced by $W$ will be acting on segment AB that is in the perpendicular direction to the component of the force. Thus, one needs to find out the length of segment AB.
The length of segment OC is given by R and the length of segment BC will be $h$ . Therefore, length of OB will be $\left( {R - h} \right)$ . Length OA is the radius of the circular cylinder. Therefore, the length of OA will be $R$ .
Thus, the length of AB will be:
${(OA)^2} = {(OB)^2} + {(AB)^2} \to {(AB)^2} = {(OA)^2} - {(OB)^2}$
Therefore, ${(AB)^2} = {(R)^2} - {(R - h)^2} = {R^2} - {R^2} + 2Rh - {h^2}$
Thus, $AB = \sqrt {2Rh - {h^2}}$
Therefore, the torque produced by the weight of the cylinder will be
${\tau _2} = W\sqrt {2Rh - {h^2}}$ $\to (2)$
Balancing the torques ${\tau _1}$ and ${\tau _2}$ . That is, equating equations (1) and (2)
$F\left( {2R - h} \right) = W\sqrt {2Rh - {h^2}} \to F = \dfrac{{W\sqrt {2Rh - {h^2}} }}{{\left( {2R - h} \right)}}$
Therefore, the minimum force $F$ necessary to raise the cylinder is $\dfrac{{W\sqrt {2Rh - {h^2}} }}{{\left( {2R - h} \right)}}$ .

Note:
The weight of the cylinder $W$ can also be written as $mg$ , where $m$ is the mass of cylinder and $g$ is the acceleration due to gravity.
Note that the force $F = \dfrac{{W\sqrt {2Rh - {h^2}} }}{{\left( {2R - h} \right)}}$ is only the minimum force that is needed to raise the cylinder just to the height $h$ . As the cylinder has to climb the step and does not slip over the step, frictional force is not considered.