Question

A cylinder of radius R full of liquid of density$\rho$is rotated about its axis at $\omega {\text{ }}rad/s$. The increase in pressure at the center of the cylinder will be
A. $\dfrac{{\rho {\omega ^2}{R^2}}}{2}$
B. $\dfrac{{\rho {\omega ^2}R}}{2}$
C. $\dfrac{{{\rho ^2}\omega R}}{2}$
D. $\dfrac{{{\rho ^2}{\omega ^2}{R^2}}}{2}$

Answer 1

Hint : The cylinder is performing rotational motion, so it will have moment of inertia and thus a torque associated with it. Find the value of torque using the equation for moment of inertia. Later deduce the value of force from torque and then pressure from force. Lastly, use the value of pressure per unit length to find the required answer.
Formula Used:
Moment of inertia of hollow cylinder: $I = M{R^2}$
Torque, $\tau = I\alpha$
Force, $F = \dfrac{\tau }{R}$
\eqalign{ & {\text{where }}M{\text{ is the mss of the cylinder,}} \cr & R{\text{ is the perpendicular distance from the rotational axis,}} \cr & {\text{I is the moment of inertia,}} \cr & \tau {\text{ is the Torque,}} \cr & \alpha {\text{ is the angular acceleration,}} \cr & A{\text{ is the area of cylinder}}{\text{.}} \cr}

Complete step by step answer:
The moment of inertia of a body is its tendency to resist change which causes rotational motion in it, i.e. the angular acceleration. It is mathematically given as the product of the mass of the body and its radius of gyration.
For a hollow cylinder its moment of inertia about its axis of rotation is give as:
$I = M{R^2}$

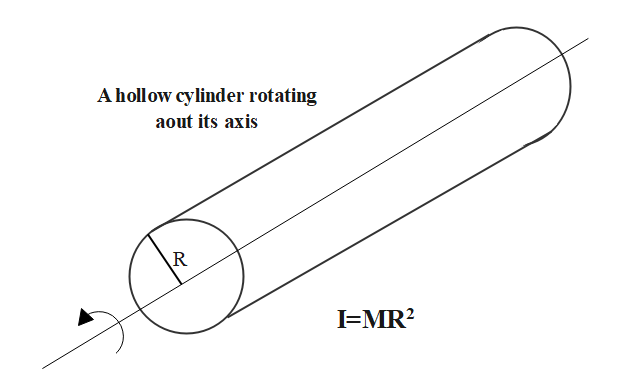
When this cylinder is filled up completely with a liquid of density $\rho$ and then rotated about the same axis with angular velocity$\omega {\text{ }}rad/s$.
Then the moment of inertia of the cylinder will change to become:
$I' = M{R^2} + \dfrac{1}{2}\pi {R^2}l\rho \times {R^2}$
where $\pi {R^2}l\rho$ is the mass of the cylinder with the liquid.
So, the increase in the torque acting on the hollow cylinder is:
\eqalign{ & \tau = \left( {I' - I} \right)\alpha {\text{ }}\left[ {\because \tau = I\alpha } \right] \cr & \tau = \dfrac{{\pi {R^2} \times {R^2}}}{2}\alpha \cdots \cdots \cdots \cdots \left( 1 \right) \cr}
But we know that angular acceleration $\alpha$ is related to angular velocity $\omega$ by:
$\alpha = \dfrac{{d\omega }}{{dt}}$
Substituting value of angular velocity in equation (1), we get:
$\tau = \dfrac{{\pi {R^2}l\rho \times {R^2}}}{2} \times \dfrac{{d\omega }}{{dt}}$
But
\eqalign{ & \tau = F \times R \cr & \Rightarrow F = \dfrac{\tau }{R} \cr & \Rightarrow F = \dfrac{{\pi {R^4}l\rho \alpha }}{{2R}} \cdots \cdots \cdots \cdots (2) \cr}
Also, linear acceleration is related to angular acceleration by:
$a = R\alpha = \dfrac{{{v^2}}}{R}$
Substituting its value in equation(2) we get:
\eqalign{ & F = \dfrac{{\pi {R^3}l\rho {v^2}}}{{2{R^2}}} \cr & \Rightarrow F = \dfrac{{\pi {R^3}l\rho {\omega ^2}}}{2} \cr}
Now, the increase in pressure at the center of the cylinder will be:
\eqalign{ & P = \dfrac{F}{A} = \dfrac{{\pi {R^3}l\rho {\omega ^2}}}{{2\pi {R^2}}} \cr & P = \dfrac{{Rl\rho {\omega ^2}}}{2} \cr}
This pressure per unit length of the cylinder will be:
$P = \dfrac{{R\rho {\omega ^2}}}{2}$
Therefore, the correct option is B. i.e., the increase in pressure at the center of the cylinder will be $\dfrac{{\rho {\omega ^2}R}}{2}$

Note : In rotational motion the concept remains the same as in the translational motion. For conversion of a translational equation into rotational just convert the variables of translational motion into their respective rotational equivalent. Students can confuse between the values of moment of inertia of a hollow cylinder and a uniform solid cylinder. In order to avoid this, memorize that the solid cylinder will have half the value of the moment of inertia that of the hollow cylinder.