Question

A cylinder of radius R and length L is placed in a uniform electric field E parallel to the cylinder axis. The outward flux over the surface of the cylinder is given by
A. $2\pi {{R}^{2}}E$
B. $\dfrac{\pi {{R}^{2}}E}{2}$
C. $2\pi RLE$
D. $\pi {{R}^{2}}E$

Answer 1

Hint : Electric flux through an area is given as $\phi =\int{\overrightarrow{E}.\overrightarrow{dA}}=\int{EdA\cos \theta }$ , where $\overrightarrow{E}$ is the electric field and $\overrightarrow{dA}$ is the area vector. $\theta$ is the angle between E and dA.
For uniform electric field and constant value of $\theta$ , the flux is equal to $\phi =EA\cos \theta$ .
$\phi =\int{\overrightarrow{E}.\overrightarrow{dA}}=\int{EdA\cos \theta }$

Complete Step By Step Answer:
Electric flux through a small area is defined as the dot product of the electric field vector and the area vector at that point.
Mathematically, electric flux through an area is given as $\phi =\int{\overrightarrow{E}.\overrightarrow{dA}}=\int{EdA\cos \theta }$ , where $\overrightarrow{E}$ is the electric field and $\overrightarrow{dA}$ is the area vector. $\theta$ is the angle between E and dA.
For uniform electric field and constant value of $\theta$ , the flux is equal to $\phi =EA\cos \theta$ .
It is given that a cylinder of radius R and length L is placed in a uniform electric field E parallel to the cylinder axis.

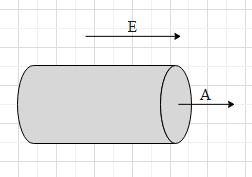
We are supposed to find the outward flux over the surface of the cylinder. As we can see in the figure, the outward flux is through the circular face of the cylinder that is at the right.
For this face, the area vector and the electric field are in the same direction. Therefore, the angle between them is zero and $\cos 0=1$ .
This means that outward flux is equal to $\phi =EA\cos 0=EA$ , where A is the area of the circular face.
Here, $A=\pi {{R}^{2}}$ .
$\phi =EA=E(\pi {{R}^{2}})=\pi {{R}^{2}}E$ .
Therefore, the outward flux over the surface of the cylinder is given by $\pi {{R}^{2}}E$ .
Hence, the correct option is D.

Note :
In this case, although the outward electric flux is non-zero, however the net electric flux through the cylinder is zero.
The outward flux is considered as positive flux and the inward flux is considered as negative flux.
There is a negative flux (inward flux) of the same magnitude through the circular face at the left.
And the flux through the curved surface of the cylinder is zero because the angle between the electric field and the area vector is 90 degrees and $\cos {{90}^{\circ }}=0$ .
Therefore, the net flux through the cylinder is zero.