Question
Question: A cylinder of mass \[m\] and radius \[r\] rolls down on a track from point A, as shown in the figure...
A cylinder of mass m and radius r rolls down on a track from point A, as shown in the figure. Assume that the friction is just sufficient to support rolling and velocity of the cylinder at point A was zero. Assume that r<<R then the reaction by the ground on the cylinder at point B is (Given acceleration due to gravity=g)
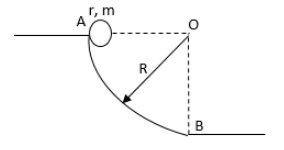
A. 37mg
B. 34mg
C. 35mg
D. 32mg
Solution
Apply law of conservation of energy to the cylinder at point A and B. Determine the value of velocity at point B from this. Calculate the acceleration of the cylinder at point B. Then apply Newton’s second law of motion to the cylinder in the vertical direction at point B and determine the reaction force.
Formulae used:
The translational kinetic energy Kt of an object is
Kt=21mv2 …… (1)
Here, m is the mass of the object and v is the velocity of the object.
The rotational kinetic energy Kr of an object is
Kr=21Iω2 …… (2)
Here, I is the moment of inertia of the object and ω is the angular speed of the object.
The potential energy U of an object is
U=mgh …… (3)
Here, m is the mass of the object, g is acceleration due to gravity and h is the height of the object from the ground.
The expression for Newton’s second law is
Fnet=ma …… (4)
Here, Fnet is the resultant force acting on the object, m is mass of the object and a is acceleration of the object.
Complete step by step answer:
We have given that the mass of the cylinder is m and radius is r and it is rolling from point A to B. The friction between the ground and the cylinder can be assumed negligible and the velocity of the cylinder at point A is zero. Draw the free body diagram of the cylinder at point B.
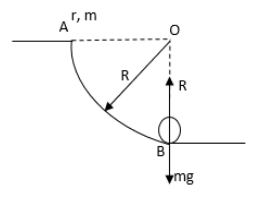
In the above figure, mg is the weight of the cylinder and R is the reaction force of the ground at point B.Apply law of conservation of energy to the cylinder at points A and B.The kinetic energy of the cylinder is zero at point A as velocity at point A is zero. The potential energy of the cylinder at point B is zero as the height of the cylinder from the ground is zero.
Hence, the potential energy UA of the cylinder at point A is equal to the kinetic energy (translational kinetic energy KtA and rotational kinetic energy KrA) of the cylinder at point B.
UA=KtA+KrA
Substitute the values of all the energies in the above equation using equations (1), (2) and (3).
mgR=21mv2+21Iω2
Here, I is the moment of inertia of the cylinder about the central axis, v is the linear velocity of cylinder at point B and ω is angular speed of cylinder at point B.
Substitute 21mR2 for I and Rv for ω in the above equation.
mgR=21mv2+21(21mR2)(Rv)2
⇒gR=21v2+41v2
⇒v2=34gR
The acceleration of the cylinder is
a=Rv2
Substitute 34gR for v2 in the above equation.
a=R34gR
⇒a=34g
Hence, acceleration of the cylinder at point B is 34g.
Apply Newton’s second law of motion on the cylinder in vertical direction.
R−mg=ma
Substitute 34g for a in the above equation.
R−mg=m34g
⇒R=34mg+mg
∴R=37mg
Therefore, the reaction force of ground on the cylinder is 37mg. Hence, the correct option is A.
Note: The students should not forget to consider the rotational kinetic energy of the cylinder while using the law of conservation of energy. If the rotational kinetic energy of the cylinder is not considered then the final answer for the reaction force will not be correct.
