Question

A cylinder of mass 10kg and radius 15cm is rolling perfectly on a plane of inclination ${{30}^{o}}$. The coefficient of static friction ${{\mu }_{s}}=0.25.$
A. How much is the force of friction acting on the cylinder?
B. What is the work done against friction during rolling?
C. if the inclination θ of the plane is increased at what value of θ does the cylinder begin to skid and not roll perfectly?

Answer 1

Draw the figure of the situation given in question and resolve the forces of mg. write expression for force we know, if object is rolling then torque must act, so write equation of torque along center of cylinder find the moment of inertia of cylinder about the center of cylinder. Put all values in the force equation. This way you will get value for question (1) work done is given as the product of force and displacement therefore calculate the displacement at the point of content and line of action. For the third question use critical condition so that the cylinder won’t skid. Put the value in critical condition and calculate the value for inclination θ.
Formula used:
$\begin{aligned} & \overrightarrow{\tau }=\overrightarrow{r}\times \overrightarrow{f} \\\ & \tau =I\alpha \\\ & I=\dfrac{m{{R}^{2}}}{2} \\\ \end{aligned}$

Complete answer:
We have given a cylinder having mass 10kg and radius 15cm which is rolling on the plane. The plane is inclined at the angle of ${{30}^{o}}$ from the horizontal surface. The coefficient of friction ${{\mu }_{s}}$ is 0.25.
First let’s draw the diagram.

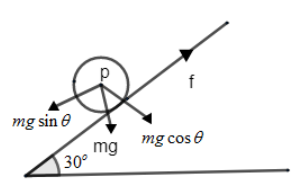
So the forces acting on the cylinder are mg which is acting downwards, normal which is acting upwards. Let’s resolve the forces of mg, which is shown in figure. Now write the expression of forces as you can see frictional force (f) is balance by $ma\sin \theta$
Therefore,
$mg\sin \theta -f=ma......\left( 1 \right)$
Now, the torque acting on cylinder is given by
$\begin{aligned} & \overrightarrow{\tau }=\overrightarrow{r}\times \overrightarrow{f} \\\ & \tau =rf\sin \theta \\\ \end{aligned}$
Since angle between radius and force is ${{90}^{o}}$ therefore torque is given as $\tau =rf$ we know that torque for circular motion is $I\alpha$
Hence $\begin{aligned} & \tau =Rf \\\ & I\alpha =Rf.......\left( 2 \right) \\\ \end{aligned}$
Where, I is the moment of inertia along the direction of torque moment of inertia passing through the center is given by $\dfrac{m{{A}^{2}}}{2}$
Then equation (2) can be written as
$\begin{aligned} & fR=\dfrac{m{{A}^{2}}}{2}a \\\ & f=\dfrac{m\alpha R}{2}.....(3) \\\ \end{aligned}$
We know that condition for pure rolling is, $v=wR$
Now differentiate w.r.to time (t)
$\begin{aligned} & \dfrac{dv}{dt}=\dfrac{dw}{st} \\\ & a=\alpha R \\\ \end{aligned}$
Put in equation (3), we get,
$f=\dfrac{ma}{2}$
Now put this value$f=\dfrac{ma}{2}$ in equation (1) we get,
$\begin{aligned} & mg\sin \theta -\dfrac{ma}{2}=ma \\\ & mg\sin \theta =\dfrac{3ma}{2}.......(4) \\\ \end{aligned}$

1. In this first part we have asked to calculate value of frictional force,
   Since $f=\dfrac{ma}{2}$
   Then equation (4) can be written as
   $mg\sin \theta =3f$
   I.e. frictional force = $\dfrac{mg\sin \theta }{3}$
   Put value of $\theta ={{30}^{o}}$
   We get, frictional force = $\dfrac{mg\sin \theta }{3}$
   $=\dfrac{10\times 9.8}{3}\times \dfrac{1}{2}$
   Frictional force = 16.33 N
   Hence, force of friction acting on the cylinder is 16.33 N
2. Now we need to calculate work done against the friction during rolling. We know that in pure rolling if the point of contact of cylinder and incline plane is P then velocity at point of contact is zero.
   $\Rightarrow \overrightarrow{{{V}_{p}}}=0$
   
   Now if the velocity at point of contact is zero then displacement of the cylinder must be zero. We know the expression for work done is given as
   $\begin{aligned} & w=F(dx) \\\ & dw=F\times 0=0 \\\ \end{aligned}$
   Since displacement along the line of action is zero.
   Hence, work done against friction during rolling is zero.
3. Now in the third part we have asked to calculate value θ. If you remember then we have to calculate value of friction as F = $\dfrac{mg\sin \theta }{3}.....(5)$
   The minimum value of friction is given as,
   ${{f}_{\max }}=\mu N=\mu mg\cos \theta$
   If value of $mg\cos \theta$ is equal to $\dfrac{mg\sin \theta }{3}$ then this is known as critical condition
   Mathematically,
   $\begin{aligned} & \mu mg\cos \theta =\dfrac{mg\sin \theta }{3} \\\ & \mu \cos \theta =\dfrac{\sin \theta }{3} \\\ & \mu =\dfrac{\tan \theta }{3} \\\ \end{aligned}$
   Value of coefficient of friction (μ) is provided i.e. 0.25
   Therefore,
   $\begin{aligned} & 0.25\times 3=\tan \theta \\\ & \tan \theta =0.75 \\\ & \tan \theta =\dfrac{3}{4} \\\ & \theta ={{\tan }^{-1}}\left( \dfrac{3}{4} \right) \\\ & \theta ={{37}^{o}} \\\ \end{aligned}$
   Hence, the value of θ is ${{37}^{o}}$ at which cylinder begins to skid.

Note:
In this equation direction of torque is the axis passing through the center of the circle and which is perpendicular to the area of the cross section. Velocity at point of contact is always zero. If the value of friction is equal to $\dfrac{mg\sin \theta }{3}$ then only pure rolling can occur. If friction is less than $\dfrac{mg\sin \theta }{3}$ then pure rolling can’t be possible if $\mu mg\cos \theta <\dfrac{mg\sin \theta }{3}$ then pure rolling can’t be possible i.e. it will not roll smoothly.