Question

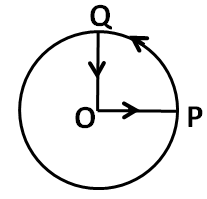
A cyclist starts from the centre O of a circular park of radius $1$ km, reaches the edge P of the park, then cycles along the circumference and returns to the centre along QO as shown in the figure. If the round trip takes ten minutes, the net displacement and average speed of the cyclist (in metre and kilometre per hour) is

(A) $0,1$
(B) $\dfrac{{\pi + 4}}{2},0$
(C) $21.4,\dfrac{{\pi + 4}}{2}$
(D) $0,21.4$

Answer 1

The displacement of a moving body is determined by measuring the distance between the initial and the final positions of the body, and its direction is from the initial to the final position. And the average speed of a body is equal to the total distance covered by it divided by the total time taken.

Complete step-by-step solution:
Let the radius of the circular park be $r$.
According to the question, the cyclist starts his journey from the centre O of the circular park. And at the end of his journey, he returns back to the centre O. This means that his initial and final positions are the same. We know that the displacement of a moving body is equal to the distance between the initial and the final positions. Since the initial and the final positions coincide, the net displacement of the cyclist is equal to zero.
Now, we know that the average speed is defined as the total distance covered divided by the total time taken. According to the question, the cyclist starts from O, travels to the edge P, then cycles along the circumference PO, and then finally returns to the centre O.
Therefore the total distance covered, as seen from the given figure, can be written as
$d = OP + PQ + OQ$
Since OP and OQ both are equal to the radius $r$ of the circular path, so we have
$d = r + PQ + r$
$\Rightarrow d = 2r + PQ$................(1)
From the given figure, OPQ is a quadrant of the circular path. Therefore, the length of PQ must be equal to the one fourth of the total circumference of the circle. Since the radius of the circle is equal to $r$ so the circumference of the circular is equal to $2\pi r$. So we have
$PQ = \dfrac{{2\pi r}}{4}$
$\Rightarrow PQ = \dfrac{{\pi r}}{2}$
Putting this in (1) we get
$d = 2r + \dfrac{{\pi r}}{2}$
The radius of the circular park is given as $1$ km. Therefore we substitute $r = 1km$ above to get
$d = 2\left( 1 \right) + \dfrac{{\pi \left( 1 \right)}}{2}$
$\Rightarrow d = \left( {2 + \dfrac{\pi }{2}} \right)km$
Putting $\pi = 3.14$ we have
$d = \left( {2 + \dfrac{{3.14}}{2}} \right)km$
$\Rightarrow d = 3.57km$.............(2)
Now, the total trip of the cyclist takes ten minutes, so the total time taken is
$t = 10\min$ ……………..(3)
We know that
$1h = 60\min$
$\Rightarrow 1\min = \dfrac{1}{{60}}h$
So (3) becomes
$t = \dfrac{{10}}{{60}}h$
$\Rightarrow t = \dfrac{1}{6}h$ ……………...(4)
From (2) and (4), the average speed of the cyclist is given by
$v = \dfrac{{3.57}}{{\dfrac{1}{6}}}km/h$
$\Rightarrow v = 3.57 \times 6km/h$
On solving, we finally get
$v = 21.42km/h$
Thus, the net displacement and the average speed of the cyclist are $0$ and $21.42$.

Hence, the correct answer is option D.

Note: We need to read carefully the units of the quantities given in the question. Then we can find our answer in which the final answers are asked.