Question
Question: A cyclist starts from the centre \(O\) of a circular park of radius \(1km\), reaches the edge \(P\) ...
A cyclist starts from the centre O of a circular park of radius 1km, reaches the edge P of the park, then cycles along the circumference and returns to the centre along QO, as shown in the figure. If the round trip takes ten minutes, the net displacement and average speed of the cyclist (in metre and kilometre per hour) are
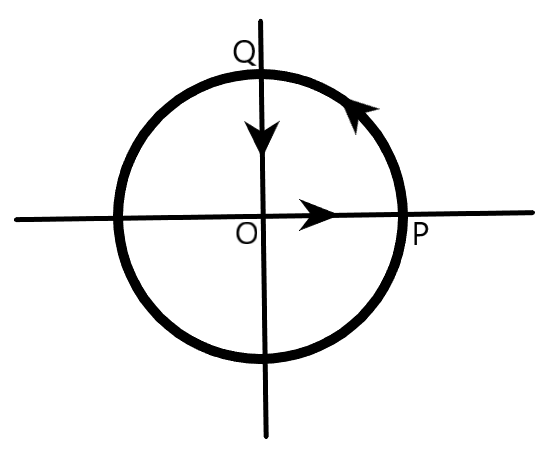
A)0,1B)2π+4,0C)21.4,2π+4D)0,21.4
Solution
Displacement of a body is defined as the distance between the final position of the body and the initial position of the body. Average speed of a body is defined as the ratio of total distance of path covered by the body to the total time taken to cover this distance.
Formula used:
1) Displacement = final position – initial position (in m)
2) Average speed = (Total distance of path) / (Total time taken) (in kmhr−1)
Complete answer:
We are provided with the information of the motion of a cyclist, in which, the cyclist starts from the centre O of a circular park of radius 1km, reaches the edge P of the park, then cycles along the circumference and returns to the centre along QO, as shown in the following figure. If the round trip takes ten minutes, we are required to calculate the net displacement (in metre) and the average speed of the cyclist (in kilometre per hour).
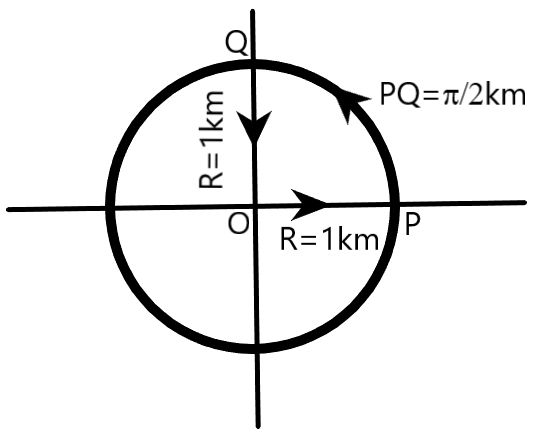
We know that displacement of a body is defined as the distance between the final position of the body and the initial position of the body. Since the initial position and the final position of the cyclist in the given question is the same (point O), the net displacement of the cyclist is equal to zero. Mathematically, displacement (d) of the cyclist can be represented as
d=0m
Let this be equation 1.
Now, we also know that the average speed of a body is defined as the ratio of total distance of path covered by the body to the total time taken to cover this distance. If Savg represents the average speed of the cyclist in the given question, then, Savg is given by
Savg=10min(OP+PQ+QO)
where
OP+PQ+QO is the total distance of the path covered by the cyclist, as clear from the figure.
10min is the total time taken by the cyclist to cover this distance, as provided in the question.
Let this be equation 2.
Here,
OP=QO=1km because these distances are equal to the radius of the circular path (R=1km), as shown in the figure
Also, it is clear from the figure that
PQ=42πR=2π×(1km)=2πkm
where
2πR=2π is the circumference of the circular path of radius R=1km
Substituting these values in equation 2, we have
Savg=10min(OP+PQ+QO)=10min1km+2πkm+1km=2hr6(π+4)km=3(π+4)kmhr−1=21.42kmhr−1
Let this be equation 3.
Therefore, from equation 1 and equation 3, the net displacement and average speed of the cyclist (in metre and kilometre per hour) are 0m and 21.42kmhr−1, respectively.
So, the correct answer is “Option D”.
Note:
Students need to be thorough with conversion formulas. Conversion formula used in this solution is:
1hr=60min1min=601hr10min=6010hr=61hr
Also, the value of π is taken as
π=3.14
