Question

A cyclist moving on a circular track of radius $40 m$ completes half a revolution in $40 sec$. Its average velocity is:
A. Zero.
B. $4\pi \,{\text{m/s}}$
C. $2 m/s$
D. $8\pi \,{\text{m/s}}$

Answer 1

The displacement of the cyclist after covering the revolution is twice the radius of the circular track. Use the formula for average velocity of the body to determine the average velocity of the cyclist.

Formula used:
The average velocity of the body is,
${v_{avg}} = \dfrac{{{x_f} - {x_i}}}{t}$
Here, ${x_f}$ is the final position, ${x_i}$ is the initial position and t is the elapsed time.

Complete step by step answer:
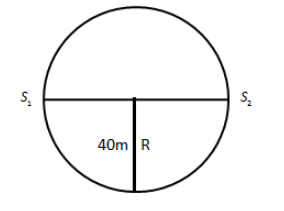
We assume the initial position of the cyclist on the circular track is ${S_1}$ and the final position on the circular track is ${S_2}$ as shown in the figure below.

We have the formula for average velocity,
${\text{Average velocity}} = \dfrac{{{\text{Displacement}}}}{{{\text{total}}\,\,{\text{time}}}}$

In the above figure, the displacement of the cyclist is, ${S_2} - {S_1}$. Since the radius of the circular track is R, the displacement of the cyclist will be 2R. Therefore, we can express the average velocity of the cyclist as,
${v_{avg}} = \dfrac{{2R}}{t}$
Here, t is the time taken by the cyclist to complete a semicircle.
Substituting 40 m for R and 40 sec for t in the above equation, we get,
${v_{avg}} = \dfrac{{2\left( {40} \right)}}{{40}}$
$\therefore {v_{avg}} = 2\,{\text{m/s}}$

Therefore, the average velocity of the cyclist is 2 m/s.So, the correct answer is option C.

Note: Displacement of the body is the difference between its final and initial position. Therefore, the displacement in this case is twice the radius. Now the term distance covered by the cyclist means the circumference of half circle. Therefore, the distance covered by the cyclist is $\pi R$. Thus, remember the difference between distance and displacement.