Question
Question: A cyclic quadrilateral ABCD of area \(\dfrac{{3\sqrt 3 }}{4}\) is inscribed in a unit circle. If one...
A cyclic quadrilateral ABCD of area 433 is inscribed in a unit circle. If one of its sides AB =1 and diagonal BD=3, find the lengths of the other sides.
Solution
Area of the quadrilateral is the sum of the areas of the two triangles which are separated by diagonal BD. Use cosine rule and sine rule of the triangle in both the triangles to evaluate the sides of the quadrilateral.
Complete step-by-step answer:
First, we draw the figure using the given information.
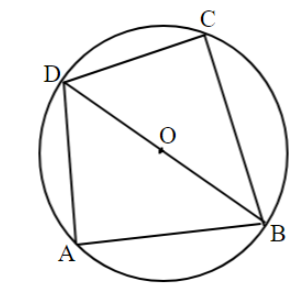
We are given that one of its sides AB =1 and diagonal BD=3.
We have to find the length of other sides.
Since, O is the centre of the circles therefore radii OA=OB=OC=OD =1.
First, we find the measure of ∠A.
Use the formula of sine rule for circumcircle radius that is,
sinABD=2R
here R is the radius of the circumcircle.
Substitute all the values and find ∠A.
sinA3=1 ⇒sinA=31 ∴A=60∘
Since the sum of opposite angles of cyclic quadrilateral is 180∘ therefore, ∠C=120∘
Now, we use cosine rule in ΔABD
cosA=2ABADAB2+AD2−BD2
Substitute all the values.
cos60∘=2AD1+AD2−3
Substitute cos60∘=21 and cross multiply to solve the equation.
Solve the quadratic equation and discard the negative value of AD.
AD2−2AD+AD−2=0 ⇒AD(AD−2)+1(AD−2)=0 ⇒(AD−2)(AD+1)=0 ∴AD=2
Now, we use cosine rule in ΔBCD
cosC=2BCDCBC2+CD2−BD2
Substitute all the values.
cos120∘=2(BC)(CD)BC2+CD2−3
Substitute cos120∘=2−1 and cross multiply to solve the equation.
We are given a cyclic quadrilateral ABCD of area 433.
Therefore,
Area of cyclic quadrilateral = Area of ΔABC+ Area of ΔBCD
Write the area of the triangle using the formula 21absinθ, here θ is the angle between the side lengths aand b.
Write the areas in the mathematical form using the above result.
433=21×1×2×sin60∘+21×BC×CD×sin120∘
Substitute sin60∘=sin120∘=21and cross multiply to solve the equation.
Substitute the value of BC×CD in the equation (1).
∴BC2+CD2+1−3=0 ⇒BC2+CD2=2..............(3)From equation (2)and (3),the only possible value of BCand CD is 1.
Therefore, the length of the other sides is AD=1 and BC=CD=1
Note: Use the sine and cosine rule of the triangle by analysing the angle and the side which includes in the rule properly.
If the length of the sides of the cyclic quadrilateral is a,b,c and d then the area of the cyclic quadrilateral will be
(s−a)(s−b)(s−c)(s−d)
Here, s=2a+b+c+d
