Solveeit Logo
Login

Question

Question: A cycle followed by an engine (made of one mole of an ideal gas in a cylinder with a piston) is show...

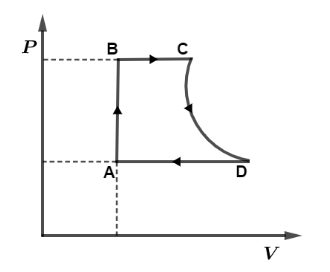
A cycle followed by an engine (made of one mole of an ideal gas in a cylinder with a piston) is shown in figure. The heat exchanged by the engine with the surroundings at constant volume is: Take (CV=32R)({C_V} = \dfrac{3}{2}R)

A. (PB−PA)VA({P_B} - {P_A}){V_A}
B. 12(PB−PA)VA\dfrac{1}{2}({P_B} - {P_A}){V_A}
C. 32[PBVB−PAVA]\dfrac{3}{2}[{P_B}{V_B} - {P_A}{V_A}]
D. 52[PBVB−PAVA]\dfrac{5}{2}[{P_B}{V_B} - {P_A}{V_A}]

Explanation

Solution

In thermodynamics, we know that a cyclic process is one in which total internal energy is zero and work done is the area under P−VP - V curve. Isobaric process is one in which pressure remains constant whereas an isochoric process is one in which volume remains constant. We will use these parameters on P−VP - V to find the heat exchanged with the surrounding.

Formula used:
First law of thermodynamics can be written mathematically as dQ=dU+dWdQ = dU + dW and dQ=CVdTdQ = {C_V}dT where CV{C_V} is known as specific heat at constant volume.
dW=PdVdW = PdV Is the work done by the gas.

Complete step by step answer:
From the given P−VP - V curve we have, process AB is isochoric which is at constant volume so, dV=0dV = 0 which means dW=0dW = 0 then by using relation, dQ=dU+dWdQ = dU + dW
dQAB=dUAB→(i)d{Q_{AB}} = d{U_{AB}} \to (i)
Now, again we can use the relation of dQ=CVdTdQ = {C_V}dT in order to find heat exchange in process AB
Q=∫TATBCVdTQ = \int\limits_{{T_A}}^{{T_B}} {{C_V}dT}
⇒Q=CV[TB−TA]\Rightarrow Q = {C_V}[{T_B} - {T_A}]
Now, it points of A and B use the ideal gas equation which is PV=nRTPV = nRT given that, n=1molen = 1mole so
For point A we have, PAVA(1R)=TA{P_A}{V_A}(\dfrac{1}{R}) = {T_A}
For point B we have, PBVB(1R)=TB{P_B}{V_B}(\dfrac{1}{R}) = {T_{_B}} put these values in equation Q=CV[TB−TA]Q = {C_V}[{T_B} - {T_A}] we get,
Q=CV[PBVB−PAVA](1R)Q = {C_V}[{P_B}{V_B} - {P_A}{V_A}](\dfrac{1}{R})
Put (CV=32R)({C_V} = \dfrac{3}{2}R) as given in the question
Q=3R2[PBVB−PAVA](1R)Q = \dfrac{{3R}}{2}[{P_B}{V_B} - {P_A}{V_A}](\dfrac{1}{R})
∴Q=32[PBVB−PAVA]\therefore Q = \dfrac{3}{2}[{P_B}{V_B} - {P_A}{V_A}]
So, the heat exchanged by the gas with surrounding at constant volume is Q=32[PBVB−PAVA]Q = \dfrac{3}{2}[{P_B}{V_B} - {P_A}{V_A}]

Hence, the correct option is C.

Note: It should be remembered that, an ideal gas is one which obeys the ideal gas equation perfectly which is written as PV=nRTPV = nRT where RR is known as the universal gas constant and it’s a fixed constant having a value of 8.314 JK−1mol−18.314\,J{K^{ - 1}}mo{l^{ - 1}} . Also work done in an isochoric process is always zero while in an isobaric process it’s written as Wisobaric=P(V2−V1){W_{isobaric}} = P({V_2} - {V_1}) .