Question

A curve $y=m{{e}^{\sin x}}$ where m>0 intersects y-axis at a point P. What is the slope of the curve at the point of intersection P?

Answer 1

Hint : First, before proceeding for this, we must know the following formula to calculate the derivative of the exponential function. Then, by using the same concept of the chain rule to the given function, we get the desired answer.

Complete step-by-step answer :
In this question, we are supposed to find the slope of the curve whose equation is given as $y=m{{e}^{\sin x}}$ shown in the graph where P is the point which cuts the y-axis.

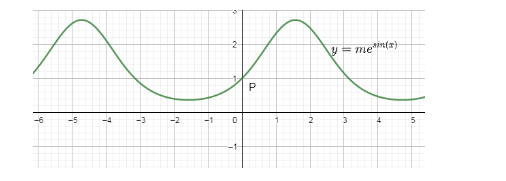
So, before proceeding for this, we must know the following formula to calculate the derivative of the exponential function.
Now, let us consider any exponential function as ${{e}^{ax}}$ .
Then, to get the derivative of the above exponential function we have:
$\dfrac{d}{dx}\left( {{e}^{ax}} \right)=a{{e}^{ax}}$
Now, by using the same concept of the chain rule to the given function.
Also, we will get to know another factor that the slope of the curve is always the derivative of the given function.
So, the slope of the given function as $y=m{{e}^{\sin x}}$ where m>0 is :
$\dfrac{dy}{dx}=\dfrac{d}{dx}\left( m{{e}^{\sin x}} \right)$
Then, by solving for the value of slope of the function by using the chain rule as:
$\begin{aligned} & \dfrac{dy}{dx}=m{{e}^{\sin x}}\times \dfrac{d}{dx}\left( \sin x \right) \\\ & \dfrac{dy}{dx}=m\cos x{{e}^{\sin x}} \\\ \end{aligned}$
So, by calculation we get the slope as $m\cos x{{e}^{\sin x}}$ .
Hence, the slope of the function $y=m{{e}^{\sin x}}$ is $m\cos x{{e}^{\sin x}}$ .

Note : Now, to solve these types of questions we need to know some of the basic derivatives of the function to get the answer appropriately. So, some of the most important derivatives of the function are as:
$\begin{aligned} & \dfrac{d}{dx}\left( \sin x \right)=\cos x \\\ & \dfrac{d}{dx}\left( \cos x \right)=-\sin x \\\ & \dfrac{d}{dx}\left( {{e}^{x}} \right)={{e}^{x}} \\\ \end{aligned}$
Moreover, we must be careful while applying the chain rule so that we will not miss any term till the end. As in the above question we may write $m{{e}^{\sin x}}$ as the final slope and forget to take the derivative of the function $\sin x$ .