Question

A curve in the shape of a quadrant of a circle has n posts, at its end and at equal distances along the curve. A man stationed at a point on one of the extreme radii produced sees the ${{p}^{th}}$ and ${{q}^{th}}$ post from the end nearest to him in a straight line. Show that the radius of the circle is $\dfrac{b}{2}\cos (p+q)\phi \cos ec\,\,p\phi \,\,\cos ec\,\,q\phi$ where $\phi \text{=}\dfrac{\pi }{4\left( n-1 \right)}$ and b is the distance of the man from the nearest end of the curve

Answer 1

To solve this question, we are going to use the fact that if there are three points in a straight line then the slope of the formed by three points is equal to the slope of the line formed by three points.

Complete step-by-step answer:
In the question, it is given that there are n posts on the circumference of the quadrant. Let us consider n=2 then the angle subtended by these posts on the center will be $\dfrac{\pi }{2}$ similarly, if n=3, then the angle becomes $\dfrac{\pi }{4}=\dfrac{\pi }{2\left( 3-1 \right)}$ Now if there are n posts then the angle subtended by two consecutive posts on center is $\dfrac{\pi }{2\left( n-1 \right)}$
Now, it is given that there is a point in the extended radius at a distance 'b' from the nearest end of the curve. It is also given that there are two points’ p and q such that the point p, point q and the point on the extended radius is a straight line. Thus, the curve will be as shown:

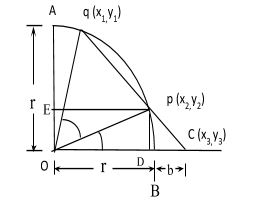
From the above figure, we can see that the radius of the quadrant is r. The value of angle $POC=\alpha$ the value of angle $QOP=\beta .$ In our case, the value of $\alpha$will be $\Rightarrow \text{ p}\times \dfrac{\pi }{2\left( n-1 \right)}$ Similarly the value of $\beta \text{=}\dfrac{(p-q)\pi }{2\left( n-1 \right)}$ .Here, we are going to make use of the concept that the slopes of the points of the line pq is equal to the slope of the points of the line PC. But we do not know the coordinates of these points. So, we consider as origin, OA as y-axis and OC as x-axis Thus, the points ${{x}_{3}}=r+b$ and ${{y}_{3}}=0$ Also the coordinates of points p and q can be calculated by the help of the angle $\alpha$and$\beta$. Therefore, the x-coordinates of the P can be calculated by dropping a perpendicular from point to the x-axis. From the triangle OPD, $\text{OD=}\,{{\text{x}}_{2}}\,=OP\,\cos \alpha \,=\,r\cos \alpha$ Similarly we will drop a perpendicular from on y-axis. Thus $\text{OE = }{{\text{y}}_{2}}\,=\,OP\,\sin \alpha \,=\,r\sin \,\alpha$ Hence, we get $\text{P(}{{\text{x}}_{2}},{{y}_{2}})=P\,(\,r\,\cos \,\alpha ,\,r\,\sin \,\alpha )$ similarly, the coordinates of the point q will be $\text{q}\left( r\cos \,\left( \alpha +\beta \right),\,r\sin \left( \alpha +\beta \right) \right)$ now we will equate the slope
Slope of line qp = slope of line PC
We know that, slope of line is given by the formula $\Rightarrow \dfrac{{{y}_{2-}}{{y}_{1}}}{{{x}_{2-}}{{x}_{1}}}\text{ }$
Thus, we get the following result: $\dfrac{{{y}_{1-}}{{y}_{2}}}{{{x}_{1-}}{{x}_{2}}}\text{ = }\dfrac{{{y}_{2-}}{{y}_{3}}}{{{x}_{2-}}{{x}_{3}}}\text{ }$
Now, we will put the values of ${{x}_{1}},{{x}_{2}},{{x}_{3}}\text{,}{{y}_{1}},{{y}_{2}}\text{ and }{{y}_{3}}$ in the above equation. Thus, we will get:
$\Rightarrow \dfrac{r\,\sin \,\left( \alpha +\beta \right)-r\,\sin \alpha }{r\,\cos \,\left( \alpha +\beta \right)-r\,\cos \alpha }\,=\,\dfrac{r\,\sin \,\alpha -O}{r\,\cos \alpha -\left( r+b \right)}$
On dividing the numerator and denominator by r on both sides, we will get:
$\Rightarrow \dfrac{\,\sin \,\left( \alpha +\beta \right)-\,\sin \alpha }{\cos \,\left( \alpha +\beta \right)-\cos \alpha }\,=\,\dfrac{\sin \alpha }{\,\cos \alpha -\left( 1+\dfrac{b}{r} \right)}\,\ldots \ldots \ldots \ldots \left( \text{i} \right)$
Now, we will take the reciprocal of above equation:
$\Rightarrow \dfrac{\,\cos \,\left( \alpha +\beta \right)-\,\cos \alpha }{\sin \left( \alpha +\beta \right)-\sin \alpha }\,\,=\,\,\dfrac{\,\,\cos \alpha -\left( 1+\dfrac{b}{r} \right)}{\sin \alpha }\ldots \ldots \ldots \ldots \left( \text{ii} \right)$
Now, we will apply following identities on left hand side of (ii):

& \Rightarrow \cos A-\,\cos B\,=\,-2\sin \left( \dfrac{A+B}{2} \right)\sin \left( \dfrac{A-B}{2} \right) \\\ & \Rightarrow \sin A\,-\,\sin B\,=\,\,2\,\cos \left( \dfrac{A+B}{2} \right)\sin \left( \dfrac{A-B}{2} \right) \\\ \end{aligned}$$ Thus, we will get the following equation: $$\begin{aligned} & \Rightarrow \,\dfrac{\,-2\sin \,\left( \dfrac{\alpha +\beta +\alpha }{2} \right)\sin \,\left( \dfrac{\alpha +\beta -\alpha }{2} \right)}{\,\,\,\,\,\,\,\cos \,\left( \dfrac{\alpha +\beta +\alpha }{2} \right)\sin \,\left( \dfrac{\alpha +\beta -\alpha }{2} \right)}\,=\,\dfrac{\cos \alpha -\,\left( 1+\dfrac{b}{r} \right)}{\sin \alpha } \\\ & \Rightarrow \dfrac{-\sin \,\left( \alpha +\dfrac{\beta }{2} \right)\sin \,\left( \dfrac{\beta }{2} \right)}{\,\,\cos \,\left( \alpha +\dfrac{\beta }{2} \right)\sin \,\left( \dfrac{\beta }{2} \right)}\,\,\,\,\,=\,\,\dfrac{\cos \alpha \,-\left( 1+\dfrac{b}{r} \right)}{\sin \alpha } \\\ \end{aligned}$$ Now, we will convert $$\sin \,\left( \dfrac{\beta }{2} \right)$$ from numerator and denominator on LHS. Thus, we will get: $$\Rightarrow \dfrac{-\sin \,\left( \alpha +\dfrac{\beta }{2} \right)}{\,\,\cos \,\left( \alpha +\dfrac{\beta }{2} \right)}\,\,\,\,\,=\,\,\dfrac{\cos \alpha \,-\left( 1+\dfrac{b}{r} \right)}{\sin \alpha }$$ Now, we know that $$\dfrac{\sin \theta }{\cos \theta }=\tan \theta $$ In our case $$\theta =\left( \alpha +\dfrac{\beta }{2} \right)$$ Thus, we have: $$\Rightarrow \,-\tan \,\left( \alpha +\dfrac{\beta }{2} \right)\,=\,\dfrac{\cos \alpha \,-\left( 1+\dfrac{b}{r} \right)}{\sin \alpha }$$ On cross multiplication, we will get: $$\begin{aligned} & \Rightarrow \,-\tan \,\left( \alpha +\dfrac{\beta }{2} \right)\,\sin \alpha =\,\cos \alpha \,-\left( 1+\dfrac{b}{r} \right) \\\ & \Rightarrow \,\,\left( 1+\dfrac{b}{r} \right)\,\,=\,\,\tan \,\left( \alpha +\dfrac{\beta }{2} \right)\,\sin \alpha \,+\,\cos \alpha \,\ldots \ldots \ldots \ldots \left( \text{iii} \right) \\\ \end{aligned}$$ Now we will convert tan in terms of sine and cosine in above equation: $$\begin{aligned} & \Rightarrow \,\,\left( 1+\dfrac{b}{r} \right)\,\,=\,\dfrac{\sin \,\left( \alpha +\dfrac{\beta }{2} \right)\,\sin \,\alpha \,+\,\cos \alpha }{\,\,\cos \,\left( \alpha +\dfrac{\beta }{2} \right)}\, \\\ & \Rightarrow \,\,\left( 1+\dfrac{b}{r} \right)\,\,=\,\dfrac{\sin \,\left( \alpha +\dfrac{\beta }{2} \right)\,\sin \,\alpha \,+\,\cos \alpha \,\cos \left( \alpha +\dfrac{\beta }{2} \right)}{\,\,\cos \,\left( \alpha +\dfrac{\beta }{2} \right)} \\\ \end{aligned}$$ Here we are going to apply the identity as shown: $$\cos A\,\cos B\,+\,\sin \,A\,+\sin \,B\,=\,\,\cos \,\left( A-B \right)$$ $$\begin{aligned} & \Rightarrow \left( 1+\dfrac{b}{r} \right)\,\,=\,\dfrac{\cos \left( \alpha +\dfrac{\beta }{2}-\alpha \right)}{\cos \left( \alpha +\dfrac{\beta }{2} \right)} \\\ & \Rightarrow \,\,\,\,1+\dfrac{b}{r}\,\,\,\,=\,\dfrac{\cos \dfrac{\beta }{2}}{\cos \left( \alpha +\dfrac{\beta }{2} \right)} \\\ & \Rightarrow \,\dfrac{b}{r}\,\,\,=\,\dfrac{\cos \dfrac{\beta }{2}}{\cos \left( \alpha +\dfrac{\beta }{2} \right)}\,-\,1 \\\ & \Rightarrow \,\,\dfrac{b}{r}\,\,\,=\,\dfrac{\cos \dfrac{\beta }{2}-\cos \left( \alpha +\dfrac{\beta }{2} \right)}{\cos \left( \alpha +\dfrac{\beta }{2} \right)}\,-\,1\ldots \ldots \ldots \ldots \left( \text{iv} \right) \\\ \end{aligned}$$ Here we are going to apply the identity as shown: $$\begin{aligned} & \,\cos A\,-\cos B\,=-2\sin \left( \dfrac{A+B}{2} \right)\sin \left( \dfrac{A-B}{2} \right) \\\ & \Rightarrow \dfrac{b}{r}\,\,=\,\dfrac{-2\sin \left( \dfrac{\beta }{2}+\alpha +\dfrac{\beta }{2} \right)\sin \left( \dfrac{\beta }{2}-\alpha -\dfrac{\beta }{2} \right)}{\cos \left( \alpha +\dfrac{\beta }{2} \right)} \\\ & \Rightarrow \dfrac{b}{r}\,\,=\,\dfrac{-2\sin \left( \alpha +\beta \right)\sin \left( -\alpha \right)}{\cos \left( \alpha +\dfrac{\beta }{2} \right)} \\\ & \Rightarrow \dfrac{b}{r}\,\,=\,\dfrac{2\sin \left( \alpha +\beta \right)\sin \alpha }{\cos \left( \alpha +\dfrac{\beta }{2} \right)}\ldots \ldots \ldots \ldots \left( \text{v} \right) \\\ \end{aligned}$$ Here, we have used the formula: $$\sin \left( -\theta \right)=-\sin \theta $$ $$\begin{aligned} & \Rightarrow \,r\,\,\,=\,\dfrac{\dfrac{b}{2}\cos \left( \alpha +\dfrac{\beta }{2} \right)}{\sin \left( \alpha +\beta \right)\sin \alpha }\,-\,1 \\\ & \Rightarrow r\,\,\,=\,\dfrac{b}{2}\cos \left( \alpha +\dfrac{\beta }{2} \right)\cos ec\left( \alpha +\beta \right)\cos ec\alpha \ldots \ldots \ldots \ldots \left( \text{vi} \right) \\\ \end{aligned}$$ Now, we will put the value of $\alpha $ and $\beta $in equation (vi) $$\begin{aligned} & \Rightarrow \,r\,\,\,=\,\dfrac{b}{2}\cos \left( \dfrac{p\pi }{2\left( n-1 \right)}+\dfrac{\left( q-p \right)\pi }{4\left( n-1 \right)} \right)\cos ec\left( \dfrac{p\pi }{2\left( n-1 \right)}+\dfrac{\left( q-p \right)\pi }{4\left( n-1 \right)} \right)\times cosec\left( \dfrac{p\pi }{2\left( n-1 \right)} \right) \\\ & \Rightarrow \,r\,\,\,=\,\dfrac{b}{2}\cos \left( \dfrac{\left( p+q \right)\pi }{4\left( n-1 \right)} \right)\cos ec\left( \dfrac{q\pi }{2\left( n-1 \right)} \right)\times cosec\left( \dfrac{p\pi }{2\left( n-1 \right)} \right) \\\ \end{aligned}$$ Now, we will put $$\dfrac{\pi }{4\left( n-1 \right)}=\phi $$ $$\Rightarrow \,\,r\,\,\,=\,\dfrac{b}{2}\cos \left( \left( p+q \right)\phi \right)\cos ec\left( q\phi \right)\times cosec\left( p\phi \right)$$ Hence proved. **Note:** We can also solve the above question by equating the triangle formed by the point’s p, q and c equal to zero. The area will be zero because they lie on the same line. The area of triangle will be: The area of triangle will be: $$\,\dfrac{1}{2}\left( \begin{matrix} {{x}_{1}} & {{y}_{1}} & 1 \\\ {{x}_{21}} & {{y}_{2}} & 1 \\\ {{x}_{3}} & {{y}_{32}} & 1 \\\ \end{matrix} \right)\,\,=\,0$$