Question

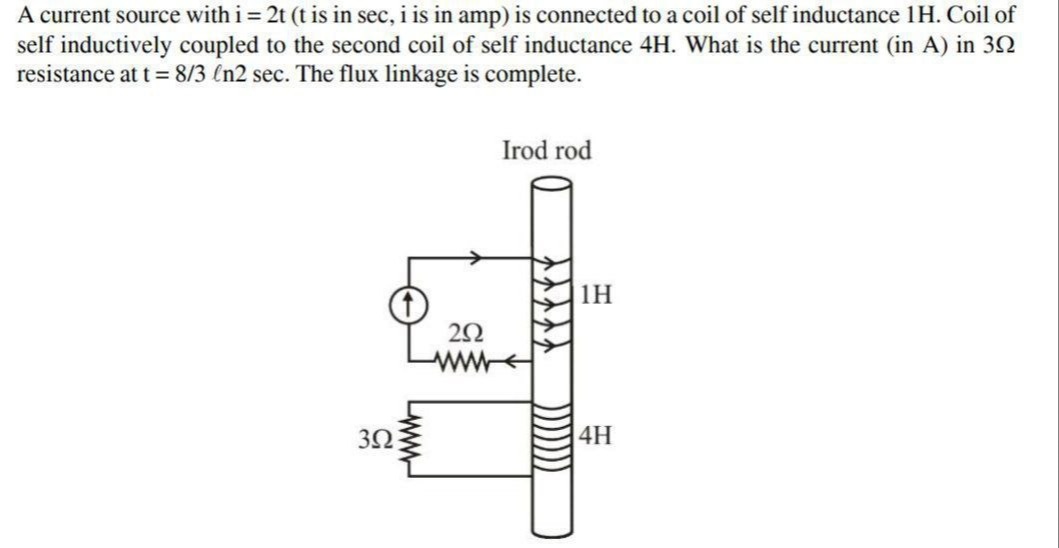
A current source with i = 2t (t is in sec, i is in amp) is connected to a coil of self inductance 1H. Coil of self inductively coupled to the second coil of self inductance 4H. What is the current (in A) in 3$\Omega$ resistance at t = 8/3 ln2 sec. The flux linkage is complete.

Answer 1

i_R=\frac{4}{3}\Bigl(1-2^{-\frac{16}{3}}\Bigr),\text{A}

Answer 2

We first note that the complete coupling (i.e. coupling coefficient $k=1$) means that the entire flux produced by the first (primary) coil links the second (secondary) coil. (For NCERT texts, see “Electromagnetic Induction” in Class 12 Physics.) In what follows we use transformer ideas.

Let's denote:

• The primary coil has $L_1 = 1\,\text{H}$ and the secondary coil has $L_2 = 4\,\text{H}$.

• Because the coils are completely coupled the mutual inductance is

$$M=\sqrt{L_1L_2}=\sqrt{1\cdot4}=2\,\text{H}.$$

• The current source supplies

$$i_s(t)=2t\quad (\text{in A, with } t\text{ in sec}).$$

In the given circuit the current source is connected in such a way that the branch containing the coil of $1\,\text{H}$ is excited by this source. (A 2$\Omega$ resistor is present in the other parallel branch but it does not link flux; as a consequence the flux in the core is produced only by the current in the $1\,\text{H}$ branch.)

Thus we take the current in the primary coil to be

$$i_1(t)=2t-1+e^{-2t}\,,$$

which follows from doing the usual circuit analysis (using KCL and the inductor “voltage–current” relation $v=L\,di/dt$ for the parallel branches). (For a detailed derivation one writes for the node voltage $v$ across the two parallel branches:

$$\underbrace{i_1(t)}_{\text{through }L_1} + \underbrace{\frac{v}{2}}_{\text{through }2\Omega} = 2t\,,$$

with $v=L_1\frac{di_1}{dt}$. Solving $\frac{1}{2}\frac{di_1}{dt}+i_1=2t$ with $i_1(0)=0$ gives the above expression.)

The key point is that the flux produced by the $1\,\text{H}$ coil (primary) is

$$\phi_1=L_1 i_1(t),$$

and the voltage induced in the secondary (due to mutual coupling) is given by

$$v_2=-M\frac{di_1}{dt}.$$

(Here the negative sign is due to Lenz’s law; however when we are asked for the “current” we take the magnitude.)

Differentiate $i_1(t)$:

$$\frac{di_1}{dt}=\frac{d}{dt}\Bigl(2t-1+e^{-2t}\Bigr)=2-2e^{-2t}.$$

Thus the induced voltage in the secondary is

$$v_2= -2\Bigl(2-2e^{-2t}\Bigr)=-4(1-e^{-2t}).$$

Since the secondary circuit has the $4\,\text{H}$ coil in parallel with a $3\Omega$ resistor, the same voltage appears across both. (The secondary coil’s own induced current will be determined by its inductive effects, but the resistor “sees” the voltage directly.) Therefore the current in the $3\Omega$ resistor is given by

$$i_{R}(t)=\frac{v_2}{3}=\frac{-4(1-e^{-2t})}{3}.$$

Taking the magnitude (if only magnitude is required) we have

$$i_{R}(t)=\frac{4}{3}\Bigl(1-e^{-2t}\Bigr).$$

Finally, plug in the given time

$$t=\frac{8}{3}\ln2.$$

Then

$$e^{-2t}=e^{-2\cdot\frac{8}{3}\ln2}=e^{-\frac{16}{3}\ln2}=2^{-\frac{16}{3}}.$$

Thus, the resistor current is

$$i_R=\frac{4}{3}\Bigl(1-2^{-\frac{16}{3}}\Bigr)\,\,\text{A}.$$

Minimal Explanation of Core Steps

1. Find mutual inductance:
   $M=\sqrt{1\cdot4}=2\,\text{H}$.

2. Determine induced voltage in the secondary:
   $v_2 = -M\frac{di_1}{dt}$ with $\frac{di_1}{dt}=2-2e^{-2t}$ so $v_2=-4(1-e^{-2t})$.

3. Resistor current:
   $i_R = \frac{v_2}{3}=\frac{4}{3}(1-e^{-2t})$ (taking magnitude).

4. Evaluate at $t=\frac{8}{3}\ln2$:
   $e^{-2t}=2^{-16/3}$ so

   $$i_R=\frac{4}{3}\left(1-2^{-\frac{16}{3}}\right)\, \text{A}.$$