Question

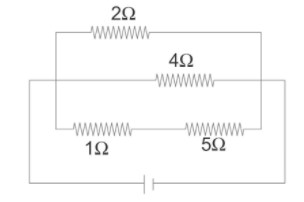
A current of ${\text{3}}\;{\text{amp}}$, flows through the $2\;\Omega$ resistor shown in the circuit. The power dissipated in the $5\;\Omega$ resistor is:

(A) $1\;{\text{watt}}$
(B) $5\;{\text{watt}}$.
(C) $4\;{\text{watt}}$.
(D) $2\;{\text{watt}}$.

Answer 1

In this question, use the concept of the parallel resistance in the circuit that is if the resistors are in parallel arrangement then the voltage difference across each resistor will be the same. Calculate the voltage of the $2\;\Omega$ resistor of the circuit. The potential of the circuit can be calculated by using Ohm’s law. This law says that voltage is directly proportional to the current.

Complete step by step answer:
In this question, we have given a circuit in which $3\;{\text{A}}$ of current is flowing through a $2\;\Omega$ resistor. We need to calculate the power dissipated in the $5\;\Omega$ resistor.

Let we denote or represent the potential by $V$ and represent the resistance of the circuit by $R$ and represent the current that is flowing in the circuit by $I$.
So, to calculate the voltage across the $2\;\Omega$ resistor, we should know Ohm's law. The Ohm’s law says that voltage or potential difference between the two points is directly proportional to the current and directly proportional to the resistance of the circuit. So,
$\Rightarrow V = IR$

Now, we calculate the voltage by substituting the values of current and resistance as,
$\Rightarrow V = 3 \times 2$

After Simplification we get,
$\Rightarrow V = 6\;{\text{V}}$
From the given diagram all the resistors are in parallel except $1\;\Omega$ and $5\;\Omega$resistors which are in series. As we know that if the resistors are in parallel arrangement then the voltage difference across each resistor will be the same.

Now, we calculate the current flowing through the $1\;\Omega$ resistor and the $5\;\Omega$ resistor.
To calculate the current in the circuit, use the Ohm’s law,
$\Rightarrow V = {I_3}{R_e}$
Here, the current flowing through the $1\;\Omega$ resistor and the $5\;\Omega$ resistor is ${I_3}$ and the equivalent resistance that is ${R_e} = 5 + 1 = 6\;\Omega$.
Now we obtain the value of current from the above expression.
$\Rightarrow {I_3} = \dfrac{V}{{{R_e}}}$
Now we substitute the values in the above equation as,
$\Rightarrow {I_3} = \dfrac{6}{{5 + 1}}$

Now, we calculate the value of current from the above expression as
$\therefore {I_3} = 1\;{\text{A}}$

The current flowing through the $1\;\Omega$ resistor and the $5\;\Omega$ resistor is $1\;{\text{A}}$. As we know that the power dissipation that is $\left( i \right)$ in a resistor is equal to the product of square of the current and the resistance.
$\Rightarrow i = I_3^2R$
Now, we substitute the values in the above expression as,
$\Rightarrow i = {1^2} \times 5$
After simplification we get,
$\therefore i = 5\;{\text{Watt}}$

Therefore, the power dissipated through the$5\;\Omega$ resistor is $5\;{\text{W}}$.
Hence, the correct option is (B).

Note: As we know that, if the resistors are in parallel the voltage across each resistor will be the same and if the resistors are in series then the current flowing through each resistor will be same and the voltage will be different.