Question

A current of $50\,A$ is passed through a straight wire of length $6\,cm$, then the magnetic induction at a point $5\,cm$ from the either end of the wire is $\left( {1\,gauss = {{10}^{ - 4\,}}\,T} \right)$
A. $2.5\,{\text{gauss}}$
B. $1.25\,{\text{gauss}}$
C. $1.2\,{\text{gauss}}$
D. $3.0\,{\text{gauss}}$

Answer 1

Hint-
Biot savart's law in the case of long straight wire has the following form
$B = \dfrac{{{\mu _0}I\left( {\sin {\theta _1} + \sin {\theta _2}} \right)}}{{4\pi x}}$
Where $B$ denotes the magnetic intensity, $I$ denotes the current,$\theta$ denotes the angle between direction of current and the line joining element to the point at a distance, $x$ denotes the distance of the point from the centre of the wire.

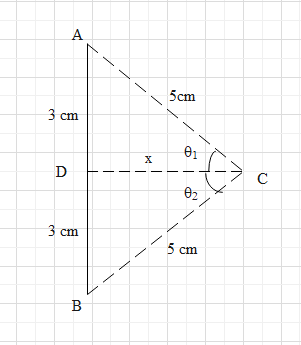
Complete step-by-step answer:
Given,
Current passing through a straight wire, $I = 50A$
Length of the wire, $l = 6\,cm$
We need to find the magnetic induction at a point $5\,cm$ from the either end of the wire.
Let us draw the diagrammatic representation. The wire is AB. Let the distance of the point from centre be x.

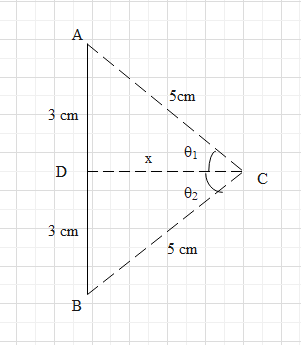
From the triangle ADC, using Pythagoras theorem we can write
$x = \sqrt {A{C^2} - A{D^2}} = \sqrt {{5^2} - {3^2}} \, = 4cm$
Now we can use Biot Savart law.
Biot savart law states that the magnetic intensity at a point due to a small current carrying element will be directly proportional to the current through the wire, length of the element, sine of angle between the direction of current and the line joining the element to the point and inversely proportional to the square of the distance of the point from the element.
$dB \propto \dfrac{{Idl\sin \theta }}{{{r^2}}}$
$dB = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{Idl\sin \theta }}{{{r^2}}}$
Where $dB$ denotes the magnetic intensity $I$ denote the current, $dl$ denotes the length of the element, $\theta$ denotes the angle between direction of current and the line joining element to the point at a distance, $r$ denotes the distance of the point from the element.
Biot savart's law in the case of long straight wire has the following form
$B = \dfrac{{{\mu _0}I\left( {\sin {\theta _1} + \sin {\theta _2}} \right)}}{{4\pi x}}$
We know,
\sin {\theta _\,} = \dfrac{{opposite\,side}}{{hypotenuse}}
therefore, $\sin {\theta _{1\,}} = \dfrac{3}{5}$
Similarly,
$\sin {\theta _2} = \dfrac{3}{5}$
Substituting the given values in the equation,
$\therefore B = \dfrac{{{\mu _0}I\left( {\dfrac{3}{5} + \dfrac{3}{5}} \right)}}{{4\pi x}}$
$B = \dfrac{{4\pi \times {{10}^{ - 7}} \times 50}}{{4\pi \times 5 \times {{10}^{ - 2}}}} \times \dfrac{6}{5} \\\ = 12 \times {10^{ - 5}}\,T \\\ = 1.2\,{\text{gauss}} \\\$

So, the correct answer is option C.

Note:
Formula to remember-
Biot savart's law in the case of long straight wire has the following form
$B = \dfrac{{{\mu _0}I\left( {\sin {\theta _1} + \sin {\theta _2}} \right)}}{{4\pi x}}$
Where $B$ denotes the magnetic intensity, $I$ denotes the current,$\theta$ denotes the angle between direction of current and the line joining element to the point at a distance, $x$ denotes the distance of the point from the centre of the wire.
\sin {\theta _\,} = \dfrac{{opposite\,side}}{{hypotenuse}}