Question

A current of 3 amp. flows through the 2 ohm resistor shown in the circuit. The power dissipated in the 5 ohm resistor is:

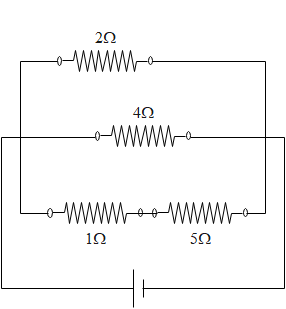
A. 1 watt
B. 5 watt
C. 4 watt
D. 2 watt

Answer 1

Hint : The power through a resistor is equal to the square of current flowing through the resistance and the resistance of the resistor. The voltages remain the same in the parallel combination while the current remains the same in the series combination. Using this information, we can obtain the required answer.
Formula used:
Ohm’s law can be given as
$V = IR$
Here V represents the potential difference or voltage, I current flowing through a circuit while R is the resistance of the circuit.

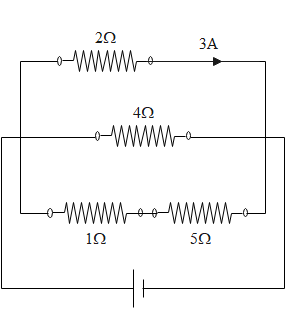
Detailed step by step solution:
We have the following circuit given to us. We can see that the current flowing through the 2 ohm resistor is equal to 3A. Since there is only one resistance in this branch of the circuit, we can calculate the voltage drop occurring in the resistor of 2ohms in the following way.

Voltage through 2$\Omega$ resistor $= 3A \times 2\Omega = 6V$
Since the voltages remain the same in the parallel combination, the voltage through the other two branches is also equal to 6V.
As we know that in series combination, voltages get divided according to the resistances of the resistor. We can find the potential drop on the 5$\Omega$ resistor can be calculated in the following way.
Voltage through 5$\Omega$ resistor $= \dfrac{{5\Omega }}{{1\Omega + 5\Omega }} \times 6V = 5V$
Hence, the current through the 5$\Omega$ resistor $= \dfrac{{5V}}{{5\Omega }} = 1A$
Now the power dissipated by the 5$\Omega$ resistor $= {\left( {1A} \right)^2} \times 5\Omega = 5W$
Hence the correct answer is option B.

Note: We have calculated the voltage through the 5$\Omega$ resistor on the basis of the fact that voltage drop for a resistor depends on the value of the resistance. The total voltage through a circuit is equal to the sum of the voltage drops across the various resistances.