Question

A current of 2 A flows through the$2\,\Omega$ resistor when connected across a battery. The same battery supplies a current of 0.5 A when connected across a $9\,\Omega$ resistor. The internal resistance of the battery is
A. $1/3\,\Omega$
B. $1/4\,\,\Omega$
C. $1\,\Omega$
D. $0.5\,\Omega$

Answer 1

Draw the circuit diagram containing external resistor and battery. Apply Kirchhoff’s voltage law and express the current in the circuit. Again express the current in the circuit for the second case and solve these two equations to determine the internal resistance of the battery.

Formula used:
Ohm’s law,
$V = IR$
Here, V is the voltage, I is the current and R is the resistance.

Complete step by step answer:
Let’s draw the circuit diagram containing battery and resistor as shown in the figure below,

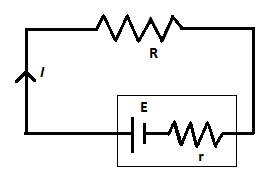
In the above figure, R is the external resistor connected across the battery and r is the internal resistance of the battery.
Now, let’s apply Kirchhoff’s voltage law to the above circuit as follows,
$E - IR - Ir = 0$
$\Rightarrow IR + Ir = E$
$\Rightarrow I = \dfrac{E}{{R + r}}$ …… (1)

This is the current in the circuit when the$2\,\Omega$ resistor is connected across the battery. Now let’s express the current in the circuit when $9\,\Omega$ resistor is connected across the battery as follows,
$I' = \dfrac{E}{{R' + r}}$ …… (2)
Dividing equation (1) and equation (2), we get,
$\dfrac{I}{{I'}} = \dfrac{{\dfrac{E}{{R + r}}}}{{\dfrac{E}{{R' + r}}}}$
$\Rightarrow \dfrac{I}{{I'}} = \dfrac{{R' + r}}{{R + r}}$
Substituting 2 A for I, 0.5 A for $I'$, $2\,\Omega$ for R and $9\,\Omega$ for $R'$ in the above equation, we get,
$\dfrac{2}{{0.5}} = \dfrac{{9 + r}}{{2 + r}}$
$\Rightarrow 4 = \dfrac{{9 + r}}{{2 + r}}$
$\Rightarrow 8 + 4r = 9 + r$
$\Rightarrow 3r = 1$
$\therefore r = 1/3\,\Omega$
Therefore, the internal resistance of the battery is $1/3\,\Omega$.

So, the correct answer is “Option A”.

Note:
In equation (2), the internal resistance of the battery r does not change with changing the value of external resistance R. Students don’t need to apply Kirchhoff’s law to express the current in the circuit. You can memorize the formula (1) to calculate the internal resistance of the battery. If multiple resistors are connected in the circuit then calculate the equivalent resistance of the circuit.