Question

A current of 2 A flows in the system of conductors as shown in the figure. The potential difference $V_P - V_R$ will be :

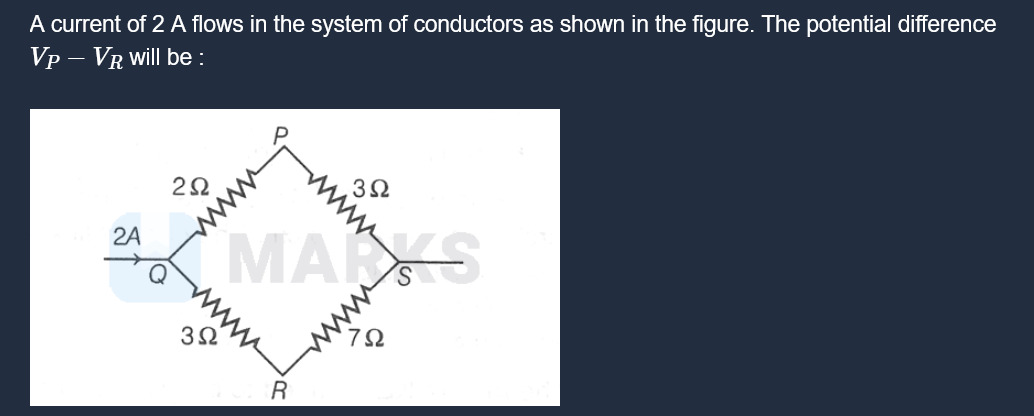
• A. 4 V
• B. 1 V
• C. 2 V
• D. 3 V

Answer 1

Answer: (A)

4 V

Answer 2

Here's how to solve this problem:

1. Circuit Analysis & Equivalent Resistances

   • The circuit has two paths from Q to R:

     • Path 1 (via P and S): Resistors in series: $R_{PQ} = 2\,\Omega$, $R_{PS} = 3\,\Omega$, and $R_{RS} = 7\,\Omega$. Total resistance = $2 + 3 + 7 = 12\,\Omega$.
     • Path 2 (Direct): A single resistor $R_{QR} = 3\,\Omega$.

2. Determine Total Voltage

   • The two branches are in parallel. Their combined (equivalent) resistance is

     $$R_{\text{eq}} = \left(\frac{1}{12} + \frac{1}{3}\right)^{-1} = \left(\frac{1}{12} + \frac{4}{12}\right)^{-1} = \left(\frac{5}{12}\right)^{-1} = \frac{12}{5} = 2.4\,\Omega.$$

   • With a total current $I = 2\,A$, the voltage between Q and R is

     $$V_Q - V_R = I \times R_{\text{eq}} = 2 \times 2.4 = 4.8\,V.$$

3. Current Division in the Branches

   • The current through the direct branch (QR) is given by current division:

     $$I_{QR} = 2 \times \frac{1/3}{1/3 + 1/12} = 2 \times \frac{1/3}{5/12} = 2 \times \left(\frac{1}{3} \times \frac{12}{5}\right) = 2 \times \frac{4}{5} = 1.6\,A.$$

   • Thus, the current through the series branch (via P-S) is

     $$I_{\text{branch}} = 2 - 1.6 = 0.4\,A.$$

4. Finding $V_P$

   • In the series branch, the drop from Q to P (across the $2\,\Omega$ resistor) is:

     $$V_{PQ} = I_{\text{branch}} \times 2 = 0.4 \times 2 = 0.8\,V.$$

   • With $V_Q = 4.8\,V$ (since $V_Q - V_R = 4.8\,V$ and taking $V_R=0\,V$), we get:

     $$V_P = V_Q - V_{PQ} = 4.8 - 0.8 = 4.0\,V.$$

5. Final Answer

   • $\displaystyle V_P - V_R = 4.0\,V$.