Question
Question: A current of 1A is flowing on the side of an equilateral triangle of side \[4.5\times {{10}^{-2}}m\]...
A current of 1A is flowing on the side of an equilateral triangle of side 4.5×10−2m. The magnetic field at the centre of the triangle will be:
A) 4×10−5Wb/m2
B) Zero
C) 2×10−5Wb/m2
D) 8×10−5Wb/m2
Solution
Magnetic field due to current carrying conductor (wire) is, B=4πrμ0i(sinϕ1+sinϕ2).
Where r is the perpendicular distance from the wire of that point,
ϕ1 and ϕ2 are angles.
Complete step by step solution:
When a current flows in a conductor or wire then produces a magnetic field around it. The magnetic field lines shape depend on the shape of the current carrying conductor. If the conductor is in the shape of a cylinder, then the magnetic field lines are circular around the wire (cylinder shape).
The magnetic field due to a finite conducting wire,
B=4πrμ0i(sinϕ1+sinϕ2)
Where r is the perpendicular distance from the wire of that point,
ϕ1 and ϕ2 are the angels.
For equilateral triangle
ϕ1=ϕ2=60∘
⇒tan30∘=2.25×10−2r
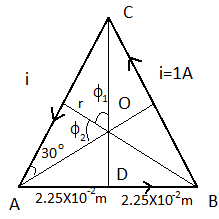
r=2.25×10−2×tan30∘
⇒r=2.25×10−2×31m
Magnetic field at the centre of the triangle due side AB,
⇒ B1=4πrμ0i(sinϕ1+sinϕ2)
Direction of the magnetic field above the plane
Magnetic field is same due to side BC and CA and direction also same,
So resultant magnetic field
B=3B1=34πrμ0i(sinϕ1+sinϕ2)
∵ϕ1=ϕ2=60∘
⇒B=3×4πrμ0i(sin60∘+sin60∘)
⇒B=3×4πrμ0i(23+23)
⇒B=3×10−7×32.25×10−21(23+3)
⇒B=2.25×10−23×10−7×3
⇒B=2.25×10−29×10−7
⇒B=4×10−5 Weber/(meter)2
Note: When we find out the magnetic field at the centre, then maximum times we take the distance from the corner but really. We should take a perpendicular distance from the write to that point.
